题目内容
（文）对于任意的平面向量
=(x1，y1)，
=(x2，y2)，定义新运算⊕：
⊕
=(x1+x2，y1y2)．若
，
，
为平面向量，k∈R，则下列运算性质一定成立的所有序号是
①
⊕
=
⊕
；
②(k
)⊕
=
⊕(k
)；
③
⊕(
⊕
)=(
⊕
)⊕
；
④
⊕(
+
)=
⊕
+
⊕
．
| a |
| b |
| a |
| b |
| a |
| b |
| c |
①③
①③
．①
| a |
| b |
| b |
| a |
②(k
| a |
| b |
| a |
| b |
③
| a |
| b |
| c |
| a |
| b |
| c |
④
| a |
| b |
| c |
| a |
| b |
| a |
| c |
分析：利用新定义和向量的线性运算即可判断出．
解答：解：①
⊕
=（x1+x2，y1y2）=(x2+x1，y2y1)=
⊕
，故正确；
②∵(k
)⊕
=（kx1+x2，ky1y2），
⊕(k
)=（x1+kx2，y1ky2），
∴(k
)⊕
≠
⊕(k
)，故不正确；
③设
=(x3，y3)，
∵
⊕(
⊕
)=
⊕（x2+x3，y2y3）=（x1+x2+x3，y1y2y3），
（
⊕
）⊕
=（x1+x2，y1y2）⊕
=（x1+x2+x3，y1y2y3），
∴
⊕（
⊕
）=（
⊕
）⊕
，故正确；
④设
=(x3，y3)，
∵
⊕(
⊕
)=
⊕（x2+x3，y2y3）=（x1+x2+x3，y1y2y3），
⊕
+
⊕
=（x1+x2，y1y2）+（x1+x3，y1y3）=（2x1+x2+x3，y1（y2+y3）），
∴
⊕（
⊕
）≠
⊕
+
⊕
，故不正确．
综上可知：只有①③正确．
故答案为①③．
| a |
| b |
| b |
| a |
②∵(k
| a |
| b |
| a |
| b |
∴(k
| a |
| b |
| a |
| b |
③设
| c |
∵
| a |
| b |
| c |
| a |
（
| a |
| b |
| c |
| c |
∴
| a |
| b |
| c |
| a |
| b |
| c |
④设
| c |
∵
| a |
| b |
| c |
| a |
| a |
| b |
| a |
| c |
∴
| a |
| b |
| c |
| a |
| b |
| a |
| c |
综上可知：只有①③正确．
故答案为①③．
点评：熟练掌握新定义和向量的线性运算是解题的关键．
练习册系列答案
第1卷单元月考期中期末系列答案
相关题目
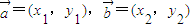，定义新运算⊕：
．若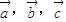
为平面向量，k∈R，则下列运算性质一定成立的所有序号是 ．
=
； 
；
； 
．
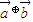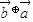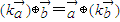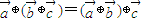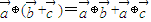与平面
，在平面
与平面
，在平面