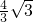题目内容
在一次抗洪抢险中,准备用射击的方法引爆从河上游漂流而下的一只巨大汽油罐.已知只有5发子弹备用,且首次命中只能使汽油流出,再次命中才能引爆成功.每次射击命中的概率都是 ,每次命中与否互相独立.
,每次命中与否互相独立.
(Ⅰ)求恰好射击5次引爆油罐的概率;
(Ⅱ)如果引爆或子弹打光则停止射击,设射击次数为ξ,求ξ的分布列及ξ的数学期望.
解:(Ⅰ)∵每次命中与否互相独立.且每次射击命中的概率都是 ,
,
∴是一个独立重复试验,
记“恰好射击5次引爆油罐”的事件为事件A,
表示前四次有一次射中且第五次一定击中,
∴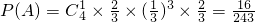 .
.
(Ⅱ)射击次数ξ的可能取值为2,3,4,5.
当ξ=2时,表示两枪都击中,
当ξ=3时,表示前两枪中有一枪击中且第三枪一定击中,
当ξ=4时,表示前三枪中有一枪击中且第四枪一定击中,
当ξ=5时,表示前四枪中有一枪击中且第五枪一定击中,
∴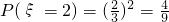 ;
;
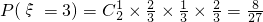 ;
;
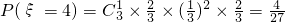 ;
;
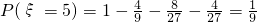 .
.
∴ξ的分布列为

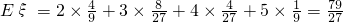 .
.
∴所求ξ的数学期望为 .
.
分析:(Ⅰ)由题意知每次命中与否互相独立.且每次射击命中的概率都是 ,本试验是一个独立重复试验,恰好射击5次引爆油罐表示前四次有一次射中且第五次一定击中,根据独立重复试验公式得到结果.
,本试验是一个独立重复试验,恰好射击5次引爆油罐表示前四次有一次射中且第五次一定击中,根据独立重复试验公式得到结果.
(2)射击次数ξ的可能取值为2,3,4,5.当ξ=2时,表示两枪都击中,当ξ=3时,表示前两枪中有一枪击中且第三枪一定击中,当ξ=4时,表示前三枪中有一枪击中且第四枪一定击中,当ξ=5时,表示前四枪中有一枪击中且第五枪一定击中,写出分布列.
点评:考查运用概率知识解决实际问题的能力,注意满足独立重复试验的条件,解题过程中判断概率的类型是难点也是重点,这种题目高考必考,应注意解题的格式.
 ,
,∴是一个独立重复试验,
记“恰好射击5次引爆油罐”的事件为事件A,
表示前四次有一次射中且第五次一定击中,
∴
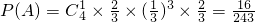 .
.(Ⅱ)射击次数ξ的可能取值为2,3,4,5.
当ξ=2时,表示两枪都击中,
当ξ=3时,表示前两枪中有一枪击中且第三枪一定击中,
当ξ=4时,表示前三枪中有一枪击中且第四枪一定击中,
当ξ=5时,表示前四枪中有一枪击中且第五枪一定击中,
∴
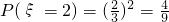 ;
;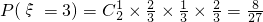 ;
;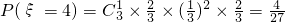 ;
;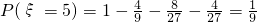 .
.∴ξ的分布列为

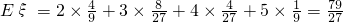 .
.∴所求ξ的数学期望为
 .
.分析:(Ⅰ)由题意知每次命中与否互相独立.且每次射击命中的概率都是
 ,本试验是一个独立重复试验,恰好射击5次引爆油罐表示前四次有一次射中且第五次一定击中,根据独立重复试验公式得到结果.
,本试验是一个独立重复试验,恰好射击5次引爆油罐表示前四次有一次射中且第五次一定击中,根据独立重复试验公式得到结果.(2)射击次数ξ的可能取值为2,3,4,5.当ξ=2时,表示两枪都击中,当ξ=3时,表示前两枪中有一枪击中且第三枪一定击中,当ξ=4时,表示前三枪中有一枪击中且第四枪一定击中,当ξ=5时,表示前四枪中有一枪击中且第五枪一定击中,写出分布列.
点评:考查运用概率知识解决实际问题的能力,注意满足独立重复试验的条件,解题过程中判断概率的类型是难点也是重点,这种题目高考必考,应注意解题的格式.

练习册系列答案
 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
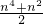 时,当n=k+1时左端在n=k时的左端加上 ________.
时,当n=k+1时左端在n=k时的左端加上 ________. ,则
,则 =
=

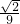
 )有最小值,则实数a的取值范围是
)有最小值,则实数a的取值范围是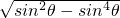 化简为
化简为