题目内容
(本题满分14分)如图:多面体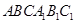 中,三角形
中,三角形 是边长为4的正三角形,
是边长为4的正三角形, ,
, 平面
平面 ,
, .
.
(1)若 是
是 的中点,求证:
的中点,求证:
 ;
;
(2)求平面 与平面
与平面 所成的角的余弦值.
所成的角的余弦值.

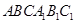 中,三角形
中,三角形 是边长为4的正三角形,
是边长为4的正三角形, ,
, 平面
平面 ,
, .
.(1)若
 是
是 的中点,求证:
的中点,求证:
 ;
;(2)求平面
 与平面
与平面 所成的角的余弦值.
所成的角的余弦值.
18.(本小题满分14分)
解:(1)设线段 的中点为
的中点为 ,由
,由 平面
平面 得:
得: ,
,
又 ,所以
,所以 是正方形,点
是正方形,点 是线段
是线段 的中点,
的中点,
所以 ,所以
,所以 ,……………………………………………………2分
,……………………………………………………2分
由 平面
平面 得:
得: ,…………………………………………………3分
,…………………………………………………3分
又 ,所以
,所以 ,且
,且 ,
,
所以:
 ,所以
,所以 ,………………………………………………5分
,………………………………………………5分
所以: 平面
平面 ,所以
,所以
 ;……………………………………6分
;……………………………………6分
(2)如图以 为原点,
为原点, 所在方向分别为
所在方向分别为 轴的正方向建立空间直角坐标系
轴的正方向建立空间直角坐标系 ,则
,则 , --------8分
, --------8分

设平面 的法向量为
的法向量为 ,则有
,则有

 ,
,
令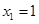 ,则
,则 …………………………10分
…………………………10分
设平面 的法向量为
的法向量为 ,则有
,则有

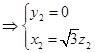 ,令
,令 ,则
,则 …………………………………12分
…………………………………12分
所以: ,
,
所以:平面 与平面
与平面 所成的角的余弦值是
所成的角的余弦值是 。…………………………14分
。…………………………14分
解:(1)设线段
 的中点为
的中点为 ,由
,由 平面
平面 得:
得: ,
,又
 ,所以
,所以 是正方形,点
是正方形,点 是线段
是线段 的中点,
的中点,所以
 ,所以
,所以 ,……………………………………………………2分
,……………………………………………………2分由
 平面
平面 得:
得: ,…………………………………………………3分
,…………………………………………………3分又
 ,所以
,所以 ,且
,且 ,
,所以:

 ,所以
,所以 ,………………………………………………5分
,………………………………………………5分所以:
 平面
平面 ,所以
,所以
 ;……………………………………6分
;……………………………………6分(2)如图以
 为原点,
为原点, 所在方向分别为
所在方向分别为 轴的正方向建立空间直角坐标系
轴的正方向建立空间直角坐标系 ,则
,则 , --------8分
, --------8分
设平面
 的法向量为
的法向量为 ,则有
,则有
 ,
,令
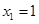 ,则
,则 …………………………10分
…………………………10分设平面
 的法向量为
的法向量为 ,则有
,则有
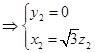 ,令
,令 ,则
,则 …………………………………12分
…………………………………12分所以:
 ,
,所以:平面
 与平面
与平面 所成的角的余弦值是
所成的角的余弦值是 。…………………………14分
。…………………………14分略

练习册系列答案
相关题目
 .
.
 ,EF =
,EF =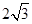 ,则另一边BC的长为何值时,二面角B-EF-D的大小为45°?
,则另一边BC的长为何值时,二面角B-EF-D的大小为45°? ,
, 是两个不同的平面,m ,n 是两条不同的直线,则下列正确的是
是两个不同的平面,m ,n 是两条不同的直线,则下列正确的是

 与平面
与平面 相交与一点A,则下列结论正确的是( )
相交与一点A,则下列结论正确的是( ) 的正视图和侧视图均是直角三角形,俯视图为矩形,N、F分别是SC、AB的中点,
的正视图和侧视图均是直角三角形,俯视图为矩形,N、F分别是SC、AB的中点,  ,
, .
.
 中,底面
中,底面 是
是 的菱形,
的菱形, ,
, ,点
,点 在棱
在棱 上,点
上,点 是棱
是棱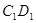 的中点;
的中点; ;
; 的长度,使得
的长度,使得 为直二面角。
为直二面角。

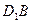 与平面
与平面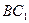 所成角的正切值
所成角的正切值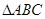 中
中 ,
, 面
面 ,
, ,求证:
,求证: 面
面 .
.