题目内容
判断函数 的奇偶性、单调性.
的奇偶性、单调性.
【答案】分析:首先求出函数的定义域,再由奇偶性的定义判断f(-x)和f(x)的关系,可利用奇函数的变形公式,求f(-x)+f(x)=0.然后先由导数判断y= 的单调性,再由复合函数的单调性确定f(x)的单调性即可.
的单调性,再由复合函数的单调性确定f(x)的单调性即可.
解答:解:因为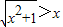 ,所以f(x)的定义域为R,
,所以f(x)的定义域为R,
因为f(-x)+f(x)= =
= =0
=0
所以f(-x)=-f(x),所以f(x)为奇函数.
令y= ,则y′=
,则y′= <0,所以y=
<0,所以y= 是减函数,
是减函数,
由复合函数的单调性知f(x)为减函数.
点评:本题考查复合函数的单调性和奇偶性的判断和证明,注意奇函数的变形公式f(-x)+f(x)=0
 的单调性,再由复合函数的单调性确定f(x)的单调性即可.
的单调性,再由复合函数的单调性确定f(x)的单调性即可.解答:解:因为
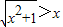 ,所以f(x)的定义域为R,
,所以f(x)的定义域为R,因为f(-x)+f(x)=
 =
= =0
=0所以f(-x)=-f(x),所以f(x)为奇函数.
令y=
 ,则y′=
,则y′= <0,所以y=
<0,所以y= 是减函数,
是减函数,由复合函数的单调性知f(x)为减函数.
点评:本题考查复合函数的单调性和奇偶性的判断和证明,注意奇函数的变形公式f(-x)+f(x)=0

练习册系列答案
相关题目

 时,有
时,有 ,求
,求 的取值范围.
的取值范围.
 的定义域为
的定义域为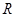 ,对任意实数
,对任意实数 ,都有
,都有 成立,且当
成立,且当 时,有
时,有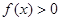 ,试判断函数
,试判断函数