题目内容
设集合M={a,1},N={b,1,2},M⊆N,a,b∈{1,2,3,…,8},且在直角坐标平面内,从所有满足这些条件的有序实数对(a,b)所表示的点中任取一个,其落在圆x2+y2=r2内的概率恰为
,则r2的所有可能的整数值是
| 1 | 3 |
30,31,32
30,31,32
.分析:根据题意,根据集合中元素的互异性,分①a=2与②a=b两种情况讨论(a,b),列举可得(a,b)的情况数目,计算可得每种情况对应a2+b2的值,分析可得,(a,b)表示的12个点中有4个点在圆的内部,8个点在圆的外部或圆上,又由a2+b2的值,分析可得r2的取值范围,进而可得r2的所有可能的整数值,即可得答案.
解答:解:根据题意,分2种情况讨论(a,b):
①、若a=2,则b可以为3、4、5、6、7、8,共6种情况,
即有序实数对(a,b)有(2,3)、(2,4)、(2,5)、(2,6)、(2,7)、(2,8),共6种情况;
②、若a=b,则a和b可取的值为3、4、5、6、7、8,共6种情况,
此时有序实数对(a,b)有(3,3)、(4,4)、(5,5)、(6,6)、(7,7)、(8,8),共6种情况;
则(a,b)的情况共有6+6=12种,
而对应a2+b2的值为13、20、29、40、53、68、18、32、50、72、98、108,也有12种情况,
如果点(a,b)落在圆x2+y2=r2内的概率恰为
,
则有4个点在圆的内部,8个点在圆的外部或圆上,
又由a2+b2的值,则29<r2≤32,故r2的所有可能的整数值为30、31、32;
故答案为30、31、32.
①、若a=2,则b可以为3、4、5、6、7、8,共6种情况,
即有序实数对(a,b)有(2,3)、(2,4)、(2,5)、(2,6)、(2,7)、(2,8),共6种情况;
②、若a=b,则a和b可取的值为3、4、5、6、7、8,共6种情况,
此时有序实数对(a,b)有(3,3)、(4,4)、(5,5)、(6,6)、(7,7)、(8,8),共6种情况;
则(a,b)的情况共有6+6=12种,
而对应a2+b2的值为13、20、29、40、53、68、18、32、50、72、98、108,也有12种情况,
如果点(a,b)落在圆x2+y2=r2内的概率恰为
| 1 |
| 3 |
则有4个点在圆的内部,8个点在圆的外部或圆上,
又由a2+b2的值,则29<r2≤32,故r2的所有可能的整数值为30、31、32;
故答案为30、31、32.
点评:本题考查概率的应用,注意借助集合中元素的互异性,由此分析点(a,b)的情况数目.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,则r2的所有可能的整数值是________.
,则r2的所有可能的整数值是________.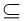 N,a,b∈{1,2,3,…,8},且在直角坐标平面内,从所有满足这些条件的有序实数对(a,b)所表示的点中任取一个,其落在圆x2+y2=r2内的概率恰为
N,a,b∈{1,2,3,…,8},且在直角坐标平面内,从所有满足这些条件的有序实数对(a,b)所表示的点中任取一个,其落在圆x2+y2=r2内的概率恰为 ,则r2的所有可能的整数值是( )
,则r2的所有可能的整数值是( )