题目内容
河道上有一座圆拱桥,在正常水位时,拱圈最高点距水面为4m,拱圈内水面宽12m,一条船在水面以上部分高2.5m,船顶部宽4m,故通行无阻,近日水位暴涨了1.7m,为此,必须加重船载,降低船身,才能通过桥洞.试问:船身应该降低多少?
分析:根据题意,以拱桥所在的圆心O为原点,建立平面直角坐标系如图所示.设桥拱所在圆的方程为x2+y2=r2,将水面未上涨时水面与拱桥的交点A(6,r-4),坐标代入圆方程算出r=
,从而得出圆方程为x2+y2=(
)2.由此算出x=2时船顶能通行的高度,由此算出水面上涨时船身的高度,结合题中数据即可算出船身应降低的距离.
| 13 |
| 2 |
| 13 |
| 2 |
解答:解:根据题意,以拱桥所在圆的圆心O为原点,
过点O垂直于水面的直线为y轴,建立平面直角坐标系,如图所示.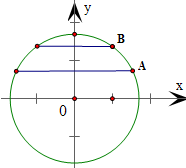
设桥拱圆的半径为r,则圆的方程为x2+y2=r2
水面未上涨时,水面与拱桥的交点为A(6,r-4),
代入圆方程,得62+(r-4)2=r2,解之得r=
∴圆方程为x2+y2=(
)2
水面未上涨时,设B点在圆周上与船顶同高,得B的纵坐标为r-4+2.5=5
设B(m,5),可得m2+52=(
)2
解之得|m|=
>2,故水面未上涨时船可以通行无阻
当x=2时,由22+y2=(
)2,解得y=
≈6.18m
由于水位暴涨了1.7m,可得船身应该降低的高度为:5+1.7-6.18=0.52m
答:在水位暴涨了1.7m的情况下船身应该降低的高度约为0.52m.
过点O垂直于水面的直线为y轴,建立平面直角坐标系,如图所示.

设桥拱圆的半径为r,则圆的方程为x2+y2=r2
水面未上涨时,水面与拱桥的交点为A(6,r-4),
代入圆方程,得62+(r-4)2=r2,解之得r=
| 13 |
| 2 |
∴圆方程为x2+y2=(
| 13 |
| 2 |
水面未上涨时,设B点在圆周上与船顶同高,得B的纵坐标为r-4+2.5=5
设B(m,5),可得m2+52=(
| 13 |
| 2 |
解之得|m|=
| ||
| 2 |
当x=2时,由22+y2=(
| 13 |
| 2 |
| ||
| 2 |
由于水位暴涨了1.7m,可得船身应该降低的高度为:5+1.7-6.18=0.52m
答:在水位暴涨了1.7m的情况下船身应该降低的高度约为0.52m.
点评:本题给出实际应用问题,求水位暴涨的情况下船身应该降低的高度,着重考查了圆的标准方程与简单几何性质和解决实际问题的数学建模等知识,属于中档题.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
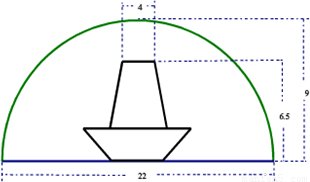
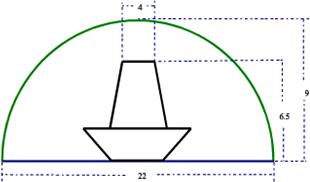 河道上有一座圆拱桥,在正常水位时,拱圈最高点距水面9m,拱圈内水面宽22m.一条船在水面以上部分高6.5m,船顶部宽4m,故通行无阻.近日水位暴涨了2.7m,为此,必须加重舰载,降低船身,才能通过桥洞.试问船身至少应该降低多少?(精确到0.01,参考数据:
河道上有一座圆拱桥,在正常水位时,拱圈最高点距水面9m,拱圈内水面宽22m.一条船在水面以上部分高6.5m,船顶部宽4m,故通行无阻.近日水位暴涨了2.7m,为此,必须加重舰载,降低船身,才能通过桥洞.试问船身至少应该降低多少?(精确到0.01,参考数据: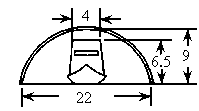
 河道上有一座圆拱桥,在正常水位时,拱圈最高点距水面9m,拱圈内水面宽22m.一条船在水面以上部分高6.5m,船顶部宽4m,故通行无阻.近日水位暴涨了2.7m,为此,必须加重舰载,降低船身,才能通过桥洞.试问船身至少应该降低多少?(精确到0.01,参考数据:
河道上有一座圆拱桥,在正常水位时,拱圈最高点距水面9m,拱圈内水面宽22m.一条船在水面以上部分高6.5m,船顶部宽4m,故通行无阻.近日水位暴涨了2.7m,为此,必须加重舰载,降低船身,才能通过桥洞.试问船身至少应该降低多少?(精确到0.01,参考数据: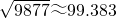 )
)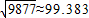 )
)