题目内容
(本题满分10分)一只小船以10 m/s的速度由南向北匀速驶过湖面,在离湖面高20米的桥上,一辆汽车由西向东以20 m/s的速度前进(如图),现在小船在水平面P点以南的40米处,汽车在桥上Q点以西30米处(其中PQ⊥水面),求小船与汽车间的最短距离(不考虑汽车与小船本身的大小).

【答案】
解:设经过时间t汽车在A点,船在B点,(如图)…………1分
则AQ=30–20t,BP=40–10t,PQ=20,且有AQ⊥BP,PQ⊥AQ,PQ⊥PB,
…………3分
设小船所在平面为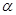 ,AQ,QP确定平面为β,记
,AQ,QP确定平面为β,记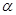 ∩β=l,由AQ∥
∩β=l,由AQ∥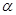 ,AQ
,AQ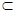 β得AQ∥l,
β得AQ∥l,
又PQ⊥水面,即PQ⊥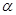 ,作AC∥PQ,则AC⊥
,作AC∥PQ,则AC⊥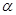 .连结CB,则AC⊥CB .
.连结CB,则AC⊥CB .
再由AQ⊥BP,CP∥AQ得CP⊥BP, …………5分
∴AB2=AC2+BC2=PQ2+PB2+PC2=202+(40–10t)2+(30–20t)2
=100[5(t–2)2+9], …………8分
t=2时AB最短,最短距离为30 m. …………10分
【解析】略

练习册系列答案
相关题目

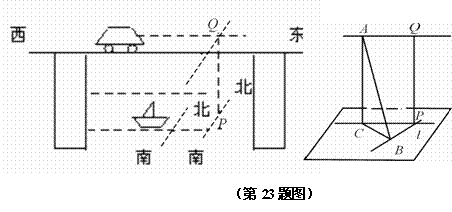 (本题满分10分)一只小船以10 m/s的速度由南向北匀速驶过湖面,在离湖面高20米的桥上,一辆汽车由西向东以20 m/s的速度前进(如图),现在小船在水平面P点以南的40米处,汽车在桥上Q点以西30米处(其中PQ⊥水面),求小船与汽车间的最短距离(不考虑汽车与小船本身的大小).
(本题满分10分)一只小船以10 m/s的速度由南向北匀速驶过湖面,在离湖面高20米的桥上,一辆汽车由西向东以20 m/s的速度前进(如图),现在小船在水平面P点以南的40米处,汽车在桥上Q点以西30米处(其中PQ⊥水面),求小船与汽车间的最短距离(不考虑汽车与小船本身的大小).