题目内容
设函数 是从1,2,3三个数中任取一个数,b是从2,3,4,5四个数中任取一个数, (1) 求
是从1,2,3三个数中任取一个数,b是从2,3,4,5四个数中任取一个数, (1) 求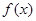 的最小值;(2)求
的最小值;(2)求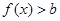 恒成立的概率.
恒成立的概率.
(1)则当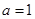 时,
时,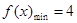 ;当
;当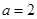 时,
时,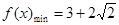 ;当
;当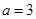 时,
时,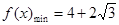 ;
;
(2) .
.
解析试题分析:(1)对于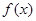 的最小值问题,对于不同的
的最小值问题,对于不同的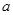 其结果不一样,故应分别讨论,且采用分离常数法;(2)由(1)小题,要使其恒成立必有
其结果不一样,故应分别讨论,且采用分离常数法;(2)由(1)小题,要使其恒成立必有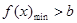 ,并由列举法计算出其中符合条件的
,并由列举法计算出其中符合条件的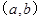 .
.
试题解析:
由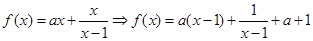 ,因为
,因为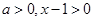 ,故有
,故有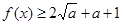 .则当
.则当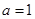 时,
时,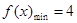 ;当
;当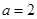 时,
时,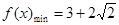 ;当
;当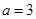 时,
时,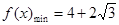 ;
;
由(1)可知,要使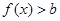 恒成立,当
恒成立,当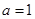 时,
时,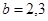 ;当
;当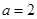 时,
时,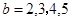 ;当
;当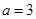 时,
时,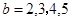 ;故满足条件的
;故满足条件的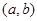 有
有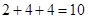 对.
对.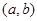 共有
共有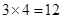 ,则概率
,则概率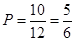 .
.
考点:(1)函数最值问题(分离常数法);(2)古典概型.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
某同学在生物研究性学习中想对春季昼夜温差大小与黄豆种子发芽多少之间的关系进行研究,于是他在4月份的30天中随机挑选了5天进行研究,且分别记录了每天昼夜温差与每天每100颗种子浸泡后的发芽数,得到如下资料:
| 日期 | 4月1日 | 4月7日 | 4月15日 | 4月21日 | 4月30日 |
温差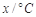 | 10 | 11 | 13 | 12 | 8 |
发芽数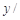 颗 颗 | 23 | 25 | 30 | 26 | 16 |
(1)从这5天中任选2天,记发芽的种子数分别为
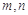 ,求事件“
,求事件“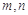 均不小于25的概率。
均不小于25的概率。(2)从这5天中任选2天,若选取的是4月1日与4月30日的两组数据,请根据这5天中的另三天的数据,求出
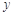 关于
关于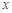 的线性回归方程
的线性回归方程 ;
;(3)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2颗,则认为得到的线性回归方程是可靠的,试问(2)中所得的线性回归方程是否可靠?(参考公式:
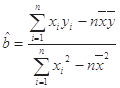 ,
,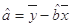 )
)  内任取一点P,则点P落在单位圆
内任取一点P,则点P落在单位圆 内的概率为 .
内的概率为 .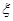 为取出的4个球中红球的个数,求
为取出的4个球中红球的个数,求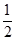 ,且各局胜负相互独立.求:
,且各局胜负相互独立.求: 的分别列与期望E
的分别列与期望E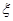 为取出的4个球中红球的个数,求
为取出的4个球中红球的个数,求