题目内容
已知数列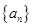 的前
的前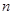 项和为
项和为 ,且满足
,且满足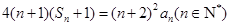 .
.
(1)求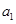 ,
,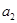 的值;
的值;
(2)求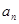 ;
;
(3)设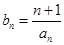 ,数列
,数列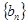 的前
的前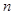 项和为
项和为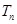 ,求证:
,求证: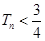 .
.
(1)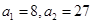 (2)
(2)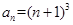 . (3)见解析
. (3)见解析
解析试题分析:
(1)分别令n=1,2,在根据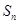 的定义即可求的
的定义即可求的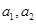 .
.
(2)利用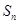 与
与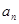 的关系(
的关系(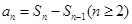 ),即可消去
),即可消去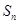 得到关于
得到关于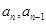 的递推式,整理可后利用叠乘法即可得到
的递推式,整理可后利用叠乘法即可得到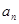 的通项公式,注意验证首项.此外还可以先找规律得到通项公式,再利用数学归纳法进行证明.这也是可以的.
的通项公式,注意验证首项.此外还可以先找规律得到通项公式,再利用数学归纳法进行证明.这也是可以的.
(3)由第二问得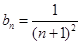 是不可求和的数列,可以考虑放缩成为可求和的数列,跟据
是不可求和的数列,可以考虑放缩成为可求和的数列,跟据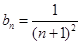 为分式,以此可以考虑放缩成为可以裂项求和的数列
为分式,以此可以考虑放缩成为可以裂项求和的数列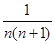 ,裂项求和即可证明相应的不等式.
,裂项求和即可证明相应的不等式.
试题解析:
(1)当 时,有
时,有 ,解得
,解得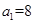 .
.
当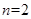 时,有
时,有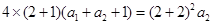 ,解得
,解得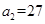 . 2分
. 2分
(2)(法一)当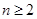 时,有
时,有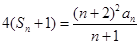 , ①
, ①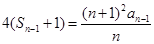 . ②
. ②
①—②得: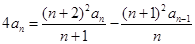 ,即:
,即: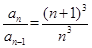 . 5分
. 5分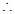
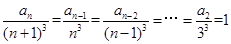 .
.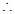
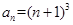
 . 8分
. 8分
另解: .
.
又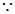 当
当 时,有
时,有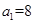 ,
, 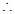
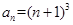 . 9分[
. 9分[
(法二)根据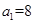 ,
,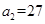 ,猜想:
,猜想: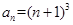 . 3分
. 3分
用数学归纳法证明如下:
(Ⅰ)当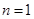 时,有
时,有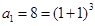 ,猜想成立.
,猜想成立.
(Ⅱ)假设当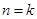 时,猜想也成立,即:
时,猜想也成立,即: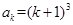 .
.
那么当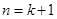 时,有
时,有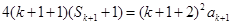 ,
,
即: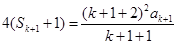 ,①
,①
又 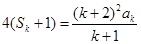 , ②
, ②
①-②得: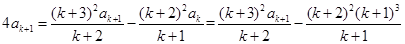 ,
,
解,得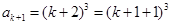 .
.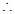 当
当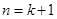 时,猜想也成立.
时,猜想也成立.
因此,由数学归纳法证得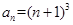 成立. 8分
成立. 8分
(3)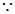
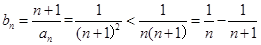 , 10分
, 10分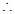
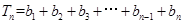

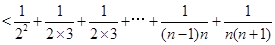

 . 14分
. 14分
考点:递推数列的通项公式、数列裂项求和公式、放缩法证明不等式等

练习册系列答案
相关题目
 的前
的前 项和为__________
项和为__________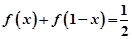 .
.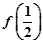 和
和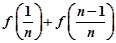 (n∈N*)的值;
(n∈N*)的值; ,求an;
,求an;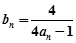 ,
,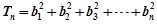 ,
,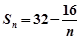 ,试比较Tn和Sn的大小。
,试比较Tn和Sn的大小。 的前
的前 项和为
项和为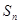 ,对一切正整数
,对一切正整数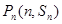 都在函数
都在函数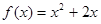 的图象上.
的图象上.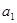 ,
,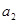 ;
;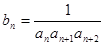 ,求证数列
,求证数列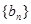 的前
的前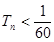 .
.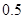 万张,同时规定一旦某年发放的牌照超过15万张,以后每一年发放的电动车的牌照的数量维持在这一年的水平不变.
万张,同时规定一旦某年发放的牌照超过15万张,以后每一年发放的电动车的牌照的数量维持在这一年的水平不变. ,每年发放的电动型汽车牌照数为构成数列
,每年发放的电动型汽车牌照数为构成数列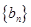 ,完成下列表格,并写出这两个数列的通项公式;
,完成下列表格,并写出这两个数列的通项公式;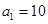
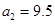
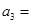
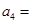
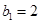

 3
3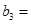
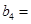
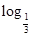 (Sn+1),求数列{bnan}的前n项和Tn.
(Sn+1),求数列{bnan}的前n项和Tn.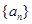 中,
中,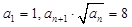 .
.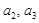 ;
;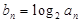 ,求证:
,求证: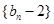 为等比数列;
为等比数列;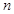 项积
项积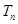 .
.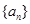 的前
的前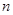 项和为
项和为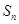 ,
,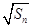 是
是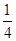 与
与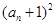 的等比中项.
的等比中项.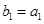 ,且
,且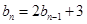 ,求数列
,求数列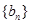 的通项公式;
的通项公式;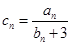 ,求数列
,求数列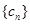 的前
的前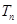 .
.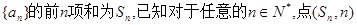 都在函数
都在函数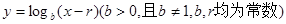 的图象上。
的图象上。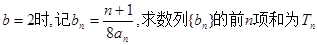 ;
;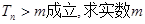 的取值范围。
的取值范围。