题目内容
(本题满分12分)
已知函数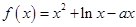 在(0,1)上是增函数.(1)求
在(0,1)上是增函数.(1)求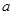 的取值范围;
的取值范围;
(2)设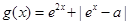 (
(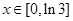 ),试求函数
),试求函数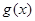 的最小值.
的最小值.
【答案】
(1)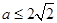 ;(2)当
;(2)当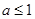 时,
时,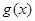 的最小值为
的最小值为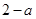 ;当
;当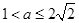 时,
时,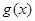 的最小值为
的最小值为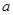 。
。
【解析】(1)本小题实质是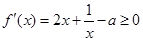 在
在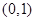 上恒成立,即转化为
上恒成立,即转化为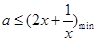 .
.
(2) 设 ,则
,则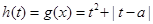 ,由
,由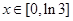 ,得
,得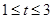 .
.
根据(1)中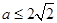 ,因此要分
,因此要分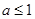 和
和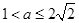 两种情况研究h(t)的最小值.
两种情况研究h(t)的最小值.
选做题(从22、23、24中选择其中一题作答.满分10分)
(1) ……2分
∵
……2分
∵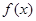 在(0,1)上是增函数
在(0,1)上是增函数
∴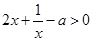 在(0,1)上恒成立,即
在(0,1)上恒成立,即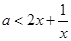 在(0,1)上恒成立
在(0,1)上恒成立
∵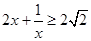 (当且仅当
(当且仅当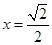 时取等号)……4分
时取等号)……4分
∴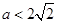 当
当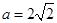 时,
时,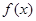 在(0,1)上也是增函数
在(0,1)上也是增函数
∴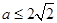 ……………………………………… 6分
……………………………………… 6分
(2)设 ,则
,则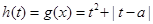
∵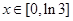 ∴
∴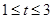
当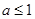 时,
时,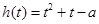 在区间
在区间 上是增函数
上是增函数
∴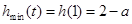 ……………………………8分
……………………………8分
当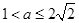 时,
时,
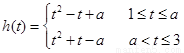 在区间
在区间 上是增函数
上是增函数
∴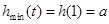 ……………………………10分
……………………………10分
综上:当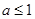 时,
时,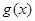 的最小值为
的最小值为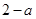 ;
;
当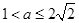 时,
时,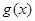 的最小值为
的最小值为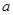 …………………………… 12分
…………………………… 12分

练习册系列答案
相关题目
 <1,xÎR }.
<1,xÎR }. ,求实数a的取值范围.
,求实数a的取值范围. (
( ,
, 为常数),且方程
为常数),且方程 有两个实根为
有两个实根为 .
. 的解析式;
的解析式; 中,四边形
中,四边形 是边长为
是边长为 的正方形,
的正方形, ,
, 为
为 上的点,且
上的点,且 ⊥平面
⊥平面
 ⊥平面
⊥平面
 的大小;
的大小; 到平面
到平面