题目内容
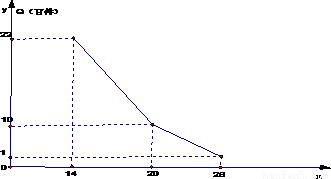
某商店经营的消费品进价每件14元,月销售量Q(百件)与销售价格P(元)的关系如图,每月各种开支2000元,(1)写出月销售量Q(百件)与销售价格P(元)的函数关系.
(2)该店为了保证职工最低生活费开支3600元,问:商品价格应控制在什么范围?
(3)当商品价格每件为多少元时,月利润并扣除职工最低生活费的余额最大?并求出最大值.
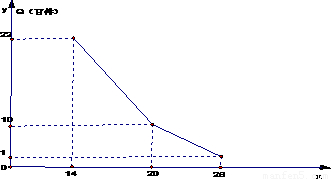
【答案】分析:(1)根据函数图象为分段函的图象,所以应求14≤P≤20,与20<x≤28两部分的解析式,由图象上的点分别代入Q=aP+b,求出即可;
(2)如果使该店刚好能够维持职工生活,那么该店经营的利润只能保证企业的全体职工每个月最低的生活费的开支3600元以及每月所需的各种开支2000元,据此列出不等关系,从而确定商品的价格;
(3)设月利润和除职工最低生活费的余额为L,列出L与售价P的函数关系式,根据函数性质求出L取最大值时,自变量P的值,从而确定商品的价格.
解答: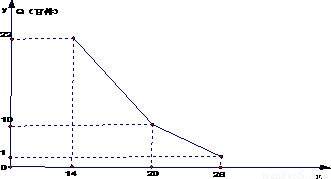 解:(1)由题设知,当14≤x≤20时,设Q=ax+b,
解:(1)由题设知,当14≤x≤20时,设Q=ax+b,
则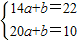 ,∴
,∴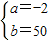
∴Q=-2x+50,
同理得,当20<x≤28时,Q=- x+40,…(4分)
x+40,…(4分)
所以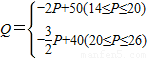 ;
;
(2)由(1)得:
Q=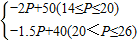 ,
,
当14≤P≤20时,(P-14)(-2P+50)×100-3600-2000≥0,
即P2-39P+378≤0,解得18≤P≤21,故18≤P≤20;
当20≤P≤26时,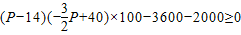 ,
,
即3P2-122P+1232≤0,解得 ,故20≤P≤22.
,故20≤P≤22.
所以18≤P≤22.
故商品价格应控制在[18,22]范围内;
(3)设月利润和除职工最低生活费的余额为L,则L=100(P-14)Q-2000.分两种情况:
第一种:当14≤P≤20时,即L=100(P-14)(-2P+50)-2000=-200P2+7800P-72000,则当P=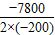 =19.5时,L有最大值,
=19.5时,L有最大值,
此时L=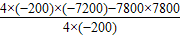 -3600=4050-3600=450;
-3600=4050-3600=450;
第二种:当20≤P≤28时,即100(P-14)(-1.5P+40)-2000=-150P2+6100P-58000,
则当P=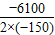 =
=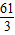 时,L有最大值,此时L=
时,L有最大值,此时L=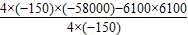 -3600=4016
-3600=4016 -3600=416
-3600=416 .
.
因为450>416 ,所以当P=19.5元时,月利润最大,为450元.
,所以当P=19.5元时,月利润最大,为450元.
点评:本题是一道综合题,难度较大.重点考查了一次函数图象和实际应用相结合的问题,能够从图象上准确地获取信息,本题中Q与P的关系是分段的,要注意对应,这是做本题的关键.
(2)如果使该店刚好能够维持职工生活,那么该店经营的利润只能保证企业的全体职工每个月最低的生活费的开支3600元以及每月所需的各种开支2000元,据此列出不等关系,从而确定商品的价格;
(3)设月利润和除职工最低生活费的余额为L,列出L与售价P的函数关系式,根据函数性质求出L取最大值时,自变量P的值,从而确定商品的价格.
解答:
 解:(1)由题设知,当14≤x≤20时,设Q=ax+b,
解:(1)由题设知,当14≤x≤20时,设Q=ax+b,则
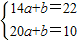 ,∴
,∴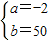
∴Q=-2x+50,
同理得,当20<x≤28时,Q=-
 x+40,…(4分)
x+40,…(4分)所以
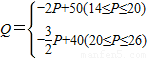 ;
;(2)由(1)得:
Q=
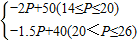 ,
,当14≤P≤20时,(P-14)(-2P+50)×100-3600-2000≥0,
即P2-39P+378≤0,解得18≤P≤21,故18≤P≤20;
当20≤P≤26时,
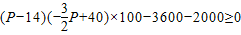 ,
,即3P2-122P+1232≤0,解得
 ,故20≤P≤22.
,故20≤P≤22.所以18≤P≤22.
故商品价格应控制在[18,22]范围内;
(3)设月利润和除职工最低生活费的余额为L,则L=100(P-14)Q-2000.分两种情况:
第一种:当14≤P≤20时,即L=100(P-14)(-2P+50)-2000=-200P2+7800P-72000,则当P=
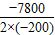 =19.5时,L有最大值,
=19.5时,L有最大值,此时L=
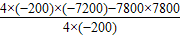 -3600=4050-3600=450;
-3600=4050-3600=450;第二种:当20≤P≤28时,即100(P-14)(-1.5P+40)-2000=-150P2+6100P-58000,
则当P=
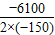 =
=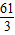 时,L有最大值,此时L=
时,L有最大值,此时L=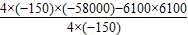 -3600=4016
-3600=4016 -3600=416
-3600=416 .
.因为450>416
 ,所以当P=19.5元时,月利润最大,为450元.
,所以当P=19.5元时,月利润最大,为450元.点评:本题是一道综合题,难度较大.重点考查了一次函数图象和实际应用相结合的问题,能够从图象上准确地获取信息,本题中Q与P的关系是分段的,要注意对应,这是做本题的关键.

练习册系列答案
相关题目
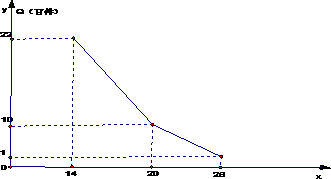
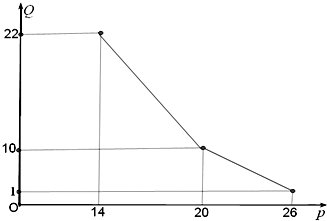 某商店经营的消费品进价每件14元,月销售量Q(百件)与销售价格p(元)的关系如下图,每月各种开支2000元.
某商店经营的消费品进价每件14元,月销售量Q(百件)与销售价格p(元)的关系如下图,每月各种开支2000元.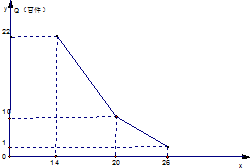 某商店经营的消费品进价每件14元,月销售量Q(百件)与销售价格P(元)的关系如图,每月各种开支2000元,
某商店经营的消费品进价每件14元,月销售量Q(百件)与销售价格P(元)的关系如图,每月各种开支2000元,