题目内容
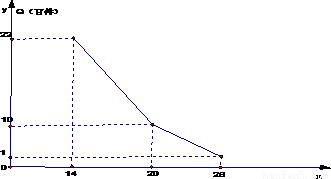
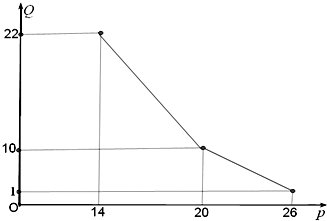 某商店经营的消费品进价每件14元,月销售量Q(百件)与销售价格p(元)的关系如下图,每月各种开支2000元.
某商店经营的消费品进价每件14元,月销售量Q(百件)与销售价格p(元)的关系如下图,每月各种开支2000元.(1)写出月销售量Q(百件)与销售价格p(元)的函数关系;
(2)写出月利润y(元)与销售价格p(元)的函数关系;
(3)当商品价格每件为多少元时,月利润最大?并求出最大值.
分析:(1)由题意可得直线的斜率,由直线方程的点斜式方程可得解析式;
(2)利润=收入-成本,结合(1)可得答案;
(3)由(2)的分段函数,分别由二次函数的最值求解各段的最大值,比较出较大的即可.
(2)利润=收入-成本,结合(1)可得答案;
(3)由(2)的分段函数,分别由二次函数的最值求解各段的最大值,比较出较大的即可.
解答:解:(1)当14≤P≤20时,直线过点(20,10),(14,22),
故可得斜率为k=
=-2,故所在直线的方程为Q-10=-2(p-20),
化简可得Q=-2p+50,同理可得,当20<P≤26时,Q=-
p+40,
故可得Q=
…(2分)
(2)结合(1)可知:当14≤P≤20时,y=100(P-14)(-2P+50)-2000
即y=-200(p2-39p+360)
当20<P≤26时,y=100(p-14)( -
p+40)-2000
即y=-50(3p2-122p+1160)…(4分)
所以y=
…(5分)
(3)由(2)的解析式结合二次函数的知识可知:
当14≤P≤20时,当p=-
=19.5时,函数取最大值4050,
当20<P≤26时,当-
=
时,函数取最大值
<4050
综上可得:当商品价格为19.5元时,利润最大,为4050元…(8分)
故可得斜率为k=
| 22-10 |
| 14-20 |
化简可得Q=-2p+50,同理可得,当20<P≤26时,Q=-
| 3 |
| 2 |
故可得Q=
|
(2)结合(1)可知:当14≤P≤20时,y=100(P-14)(-2P+50)-2000
即y=-200(p2-39p+360)
当20<P≤26时,y=100(p-14)( -
| 3 |
| 2 |
即y=-50(3p2-122p+1160)…(4分)
所以y=
|
(3)由(2)的解析式结合二次函数的知识可知:
当14≤P≤20时,当p=-
| -39 |
| 2×1 |
当20<P≤26时,当-
| -122 |
| 2×3 |
| 61 |
| 3 |
| 12050 |
| 3 |
综上可得:当商品价格为19.5元时,利润最大,为4050元…(8分)
点评:本题考查分段函数的解析式,涉及图象的作法,属基础题.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
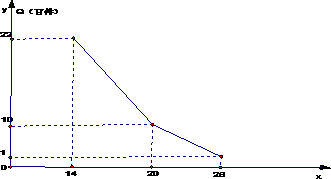
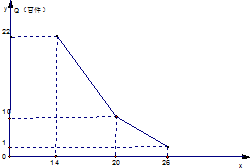 某商店经营的消费品进价每件14元,月销售量Q(百件)与销售价格P(元)的关系如图,每月各种开支2000元,
某商店经营的消费品进价每件14元,月销售量Q(百件)与销售价格P(元)的关系如图,每月各种开支2000元,