题目内容
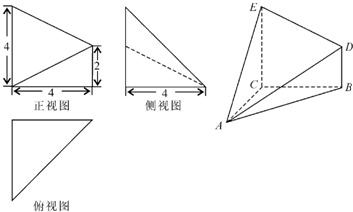
如图:正△ABC与Rt△BCD所在平面互相垂直,且∠BCD=90°,∠CBD=30°.
(1)求证:AB⊥CD;
(2)求二面角D-AB-C的正切值.
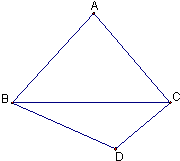
(1)求证:AB⊥CD;
(2)求二面角D-AB-C的正切值.

(1)证明:∵DC⊥BC,且平面ABC⊥平面BCD,平面ABC∩平面BCD=BC,
∴DC⊥平面ABC,
又AB?平面ABC,
∴DC⊥AB.…(5分)
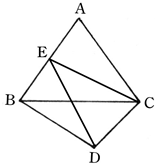
(2)过C作CE⊥AB于E,连接ED,
∵AB⊥CD,AB⊥EC,CD∩EC=C,
∴AB⊥平面ECD,
又DE?平面ECD,∴AB⊥ED,
∴∠CED是二面角D-AB-C的平面角,…(9分)
设CD=a,则BC=
=
a,
∵△ABC是正三角形,
∴EC=BCsin60°=
,
在Rt△DEC中,tan∠DEC=
=
=
.…(13分)
∴DC⊥平面ABC,
又AB?平面ABC,
∴DC⊥AB.…(5分)
(2)过C作CE⊥AB于E,连接ED,
∵AB⊥CD,AB⊥EC,CD∩EC=C,
∴AB⊥平面ECD,
又DE?平面ECD,∴AB⊥ED,
∴∠CED是二面角D-AB-C的平面角,…(9分)
设CD=a,则BC=
| a |
| tan30° |
| 3 |
∵△ABC是正三角形,
∴EC=BCsin60°=
| 3a |
| 2 |
在Rt△DEC中,tan∠DEC=
| DC |
| EC |
| a | ||
|
| 2 |
| 3 |


练习册系列答案
相关题目
 且
且 ,给出下列命题:
,给出下列命题: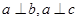 则
则 ②
②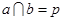 则
则
 ④若
④若 则
则