题目内容
.已知a,b均是非零向量,设a与b的夹角为θ,是否存在θ,使|a+b|= |a-b|成立,若存在,求出θ的值;若不存在,请说明理由.
|a-b|成立,若存在,求出θ的值;若不存在,请说明理由.
【答案】
θ∈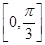 ∪
∪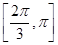 时,能使|a+b|=
时,能使|a+b|=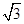 |a-b|成立
|a-b|成立
【解析】假设满足条件的θ存在,由|a+b|=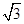 |a-b|,得(a+b)2=3(a-b)2.
|a-b|,得(a+b)2=3(a-b)2.
∴|a|2+2a·b+|b|2=3(|a|2-2a·b+|b|2),
即|a|2-4a·b+|b|2=0,
∴|a|2-4|a||b|cosθ+|b|2=0,
由Δ≥0,得(4cosθ)2-4≥0,
解得cosθ≤-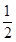 或cosθ≥
或cosθ≥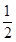 ,
,
又cosθ∈[-1,1],
∴-1≤cosθ≤-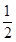 或
或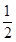 ≤cosθ≤1,
≤cosθ≤1,
∵θ∈[0,π],∴θ∈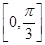 ∪
∪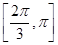 ,
,
故当θ∈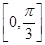 ∪
∪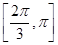 时,能使|a+b|=
时,能使|a+b|=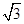 |a-b|成立.
|a-b|成立.

练习册系列答案
 全优测试卷系列答案
全优测试卷系列答案 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
已知直线
+
=1(θ是非零常数)与圆x2+y2=100有公共点,且公共点的横坐标和纵坐标均为整数,那么这样的直线共有( )
| x |
| a |
| y |
| b |
| A、60条 | B、66条 |
| C、72条 | D、78条 |