题目内容
下列函数中,最小值为2的函数是
- A.
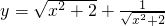
- B.
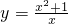
- C.
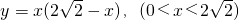
- D.
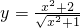
D
分析:选项A,先换元,然后利用导数研究函数的单调性从而求出最值,可判定真假;选项B,可取x=-1进行否定;选项C,利用基本不等式可求出最大值为2,可判定真假;选项C,利用基本不等式直接求解,可判定真假.
解答:选项A,令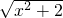 =t≥
=t≥ ,则y=t+
,则y=t+ ,t≥
,t≥ ,y′=1-
,y′=1- >0∴函数y=t+
>0∴函数y=t+ 在[
在[ ,+∞)上单调递增,则最小值为
,+∞)上单调递增,则最小值为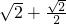 =
= ,故选项A不正确;
,故选项A不正确;
选项B,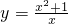 中取x=-1,则y=-2,故最小值为2不正确;
中取x=-1,则y=-2,故最小值为2不正确;
选项C,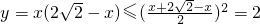 ,当且仅当x=
,当且仅当x= 取等号,故最小值为2不正确;
取等号,故最小值为2不正确;
选项D,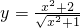 =
=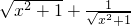 ≥2,当且仅当x=0取等号,故最小值为2正确;
≥2,当且仅当x=0取等号,故最小值为2正确;
故选D.
点评:本题主要考查了基本不等式,以及利用导数研究函数的单调性,注意利用基本不等式的条件,属于基础题.
分析:选项A,先换元,然后利用导数研究函数的单调性从而求出最值,可判定真假;选项B,可取x=-1进行否定;选项C,利用基本不等式可求出最大值为2,可判定真假;选项C,利用基本不等式直接求解,可判定真假.
解答:选项A,令
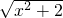 =t≥
=t≥ ,则y=t+
,则y=t+ ,t≥
,t≥ ,y′=1-
,y′=1- >0∴函数y=t+
>0∴函数y=t+ 在[
在[ ,+∞)上单调递增,则最小值为
,+∞)上单调递增,则最小值为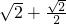 =
= ,故选项A不正确;
,故选项A不正确;选项B,
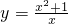 中取x=-1,则y=-2,故最小值为2不正确;
中取x=-1,则y=-2,故最小值为2不正确;选项C,
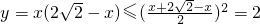 ,当且仅当x=
,当且仅当x= 取等号,故最小值为2不正确;
取等号,故最小值为2不正确;选项D,
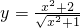 =
=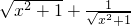 ≥2,当且仅当x=0取等号,故最小值为2正确;
≥2,当且仅当x=0取等号,故最小值为2正确;故选D.
点评:本题主要考查了基本不等式,以及利用导数研究函数的单调性,注意利用基本不等式的条件,属于基础题.

练习册系列答案
相关题目
下列函数中,最小值为2的是( )
A、y=
| ||||
B、y=lgx+
| ||||
| C、y=3x+3-x,x∈R | ||||
D、y=sin x+
|