题目内容
(本小题满分12分)
若△ABC中，a、b、c分别为内角A、B、C的对边，且1－2sinBsinC＝cos2B＋cos2C－cos2A.
(1)求A的大小；
(2)求sinB＋sinC的最值.
若△ABC中，a、b、c分别为内角A、B、C的对边，且1－2sinBsinC＝cos2B＋cos2C－cos2A.
(1)求A的大小；
(2)求sinB＋sinC的最值.
解： (1)∵1－2sinBsinC＝cos2B＋cos2C－cos2A
∴1－2sinBsinC＝1－2sin2B＋1－2sin2C－1＋2sin2A
由正弦定理可得：－2bc＝－2b2－2c2＋2a2
整理得：b2＋c2－a2＝bc(3分)
∴cosA＝＝
∴A＝60°.(6分)
(2)sinB＋sinC＝sinB＋sin(120°－B)＝sinB＋cosB＋sinB
＝cosB＋sinB＝
(cosB＋sinB)
＝sin(B＋30°)(8分)
∵0°<B<120°
∴30°<B＋30°<150°，
< sin(B＋30°)≤1，
∴<sin(B＋30°)≤
∴sinB＋sinC无最小值，最大值为.(12分)
∴1－2sinBsinC＝1－2sin2B＋1－2sin2C－1＋2sin2A
由正弦定理可得：－2bc＝－2b2－2c2＋2a2
整理得：b2＋c2－a2＝bc(3分)
∴cosA＝＝
∴A＝60°.(6分)
(2)sinB＋sinC＝sinB＋sin(120°－B)＝sinB＋cosB＋sinB
＝cosB＋sinB＝(cosB＋sinB)＝sin(B＋30°)(8分)
∵0°<B<120°
∴30°<B＋30°<150°，
< sin(B＋30°)≤1，∴<sin(B＋30°)≤
∴sinB＋sinC无最小值，最大值为.(12分)
略
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
'中，三个内角A、B, C的对边分别为a、b、c,且
，
，求
中，角A、B、C所对边分别是a、b、c，
，求
．
与
共线，其中A是△ABC的内角．
的大小； 
的最大值，并判断S取得最大值时△ABC的形状.
，则
等于（ ）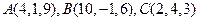
为顶点的三角形是( )
,若
,
,则A=
的大小关系是___________________________。