题目内容
如图所示,将一矩形花坛ABCD扩建成一个更大的矩形花园AMPN,要求B在AM上,D在AN上,且对角线MN过C点,|AB|=3米,|AD|=2米.

(Ⅰ)要使矩形AMPN的面积大于32平方米,则AM的长应在什么范围内?
(Ⅱ)当AM、AN的长度是多少时,矩形AMPN的面积最小?并求出最小面积.
答案:
解析:
解析:
|
解:设AM的长为x米(x>3) ∵ ∴ (Ⅰ)由SAMPN>32得 ∵ 即AM长的取值范围是(3,4) (Ⅱ)令 ∴当 ∴当x=6时, 此时|AM|=6米,|AN|=4米 答:当AM、AN的长度分别是6米、4米时,矩形AMPN的面积最小,最小面积是24平方米. 另解:以AM、AN分别为x、y轴建立直角坐标系, 设 由C在直线MN上得 ∴ ∴AM的长取值范围是(3,4) (Ⅱ)∵ ∴|AM|=6米,|AN|=4米时,SAMPN达到最小值24 |

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
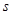 平方米,矩形一边的长为
平方米,矩形一边的长为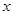 米(如图所示)
米(如图所示)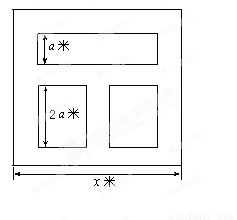
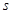 平方米,矩形一边的长为
平方米,矩形一边的长为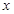 米(如图所示)
米(如图所示)