题目内容
5.过点(0,2)的直线L与双曲线x2-y2=2相交于不同两点E,F.若△OEF的面积不小于2$\sqrt{2}$.求直线L的斜率的取值范围.分析 依题意,可设直线l的方程为y=kx+2,代入双曲线C的方程并整理,得(1-k2)x2-4kx-6=0.由此入手能够求出直线l的斜率的取值范围.
解答 解:依题意,可设直线l的方程为y=kx+ 2,代入双曲线C的方程并整理,
2,代入双曲线C的方程并整理,
得(1-k2)x2-4kx-6=0.①
∵直线l与双曲线C相交于不同的两点E、F,
∴1-k2≠0,△>0,
∴k∈(-$\sqrt{3}$,$\sqrt{3}$)且k≠±1.②
设E(x1,y1),F(x2,y2),则由①式得
|x1-x2|=$\frac{2\sqrt{2}•\sqrt{3-{k}^{2}}}{|1-{k}^{2}|}$.③
当E、F在同一支上时
S△OEF=|S△ODF-S△ODE|=$\frac{1}{2}$|OD|•||x1|-|x2||=$\frac{1}{2}$|OD|•|x1-x2|;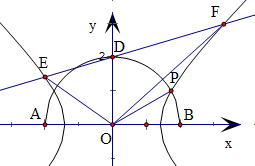
当E、F在不同支上时
S△OEF=S△ODF+S△ODE=$\frac{1}{2}$|OD|•(|x1|+|x2|)=$\frac{1}{2}$|OD|•|x1-x2|.
综上得S△OEF=$\frac{1}{2}$|OD||x1-x2|,于是由|OD|=2及③式,
得S△OEF=$\frac{2\sqrt{2}•\sqrt{3-{k}^{2}}}{|1-{k}^{2}|}$.
若△OEF面积不小于2$\sqrt{2}$,则有$\frac{2\sqrt{2}•\sqrt{3-{k}^{2}}}{|1-{k}^{2}|}$≥2$\sqrt{2}$?k2≤2,解得-$\sqrt{2}$≤k≤$\sqrt{2}$.④
综合②、④知,直线l的斜率的取值范围为-$\sqrt{2}$≤k≤$\sqrt{2}$且k≠±1.
点评 本小题主要考查直线、圆和双曲线等平面解析几何的基础知识,考查不等式的解法以及综合解题能力

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案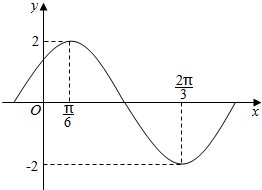 函数$f(x)=Asin(ωx+φ)\;(A>0,ω>0,|φ|<\frac{π}{2})$部分图象如图所示.
函数$f(x)=Asin(ωx+φ)\;(A>0,ω>0,|φ|<\frac{π}{2})$部分图象如图所示.