题目内容
已知函数 的定义域为M.
的定义域为M.(1)求M;
(2)当x∈M时,求f(x)=a•2x+2+3•4x(a>-3)的最小值.
【答案】分析:(1)由题意列出不等式组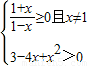 ,求出解集再用区间表示;
,求出解集再用区间表示;
(2)用配方法对解析式变形,设t=2x由(1)的结果求出t的范围,则原函数变成关于t的二次函数,再根据对称轴和t的范围进行分类,由二次函数的性质求出对应的最小值.
解答:解:(1)由题意得,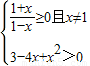 ,
,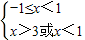 ,解得-1≤x<1
,解得-1≤x<1
∴函数的定义域M=[-1,1).
(2)f(x)=a•2x+2+3•4x)=4a•2x+3•22x=3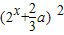 -
- a2,
a2,
由(1)知,x∈[-1,1),设t=2x,则t∈[ ,2),
,2),
函数变为g(t)=3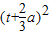 -
- a2,又∵a>-3,∴
a2,又∵a>-3,∴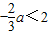 ,
,
①若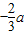 ≤
≤ 时,即a≥-
时,即a≥- ,函数g(t)在[
,函数g(t)在[ ,2)上时增函数,
,2)上时增函数,
∴f(x)的最小值是g( )=3
)=3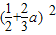 -
- a2=2a+
a2=2a+ ,
,
②若 <
<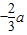 <2时,即-3<a<-
<2时,即-3<a<- ,当t=
,当t=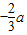 时,f(x)取到最小值是-
时,f(x)取到最小值是- a2.
a2.
综上,当a≥- 时,f(x)的最小值是2a+
时,f(x)的最小值是2a+ ;当-3<a<-
;当-3<a<- ,f(x)的最小值是-
,f(x)的最小值是- a2.
a2.
点评:本题是一道综合题,考查了求函数的定义域和最值,用了对数函数、指数函数和二次函数的性质,利用换元法对函数解析式进行转化后再求函数的最值,注意换元后的定义域和对称轴的位置.
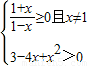 ,求出解集再用区间表示;
,求出解集再用区间表示;(2)用配方法对解析式变形,设t=2x由(1)的结果求出t的范围,则原函数变成关于t的二次函数,再根据对称轴和t的范围进行分类,由二次函数的性质求出对应的最小值.
解答:解:(1)由题意得,
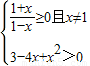 ,
,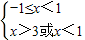 ,解得-1≤x<1
,解得-1≤x<1∴函数的定义域M=[-1,1).
(2)f(x)=a•2x+2+3•4x)=4a•2x+3•22x=3
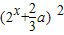 -
- a2,
a2,由(1)知,x∈[-1,1),设t=2x,则t∈[
 ,2),
,2),函数变为g(t)=3
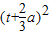 -
- a2,又∵a>-3,∴
a2,又∵a>-3,∴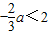 ,
,①若
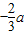 ≤
≤ 时,即a≥-
时,即a≥- ,函数g(t)在[
,函数g(t)在[ ,2)上时增函数,
,2)上时增函数,∴f(x)的最小值是g(
 )=3
)=3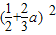 -
- a2=2a+
a2=2a+ ,
,②若
 <
<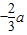 <2时,即-3<a<-
<2时,即-3<a<- ,当t=
,当t=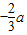 时,f(x)取到最小值是-
时,f(x)取到最小值是- a2.
a2.综上,当a≥-
 时,f(x)的最小值是2a+
时,f(x)的最小值是2a+ ;当-3<a<-
;当-3<a<- ,f(x)的最小值是-
,f(x)的最小值是- a2.
a2.点评:本题是一道综合题,考查了求函数的定义域和最值,用了对数函数、指数函数和二次函数的性质,利用换元法对函数解析式进行转化后再求函数的最值,注意换元后的定义域和对称轴的位置.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案
相关题目
 的定义域为M.
的定义域为M. 的定义域为M,函数
的定义域为M,函数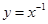 的定义域为N,则
的定义域为N,则 ( )
( ) 且
且 B.
B.  且
且 D.
D.

 的定义域为M,函数
的定义域为M,函数 的定义域为N,则
的定义域为N,则 的定义域为M,g(x)=
的定义域为M,g(x)= 的定义域为N,则M∩N=
的定义域为N,则M∩N= (B)
(B) (C)
(C) (D)
(D)