题目内容
设 分别为椭圆
分别为椭圆 的左、右两个焦点.
的左、右两个焦点.
(1)若椭圆 上的点
上的点 到
到 两点的距离之和等于4,写出椭圆
两点的距离之和等于4,写出椭圆 的方程和焦点坐标;
的方程和焦点坐标;
(2)设点 是(1)中所得椭圆上的动点,求线段
是(1)中所得椭圆上的动点,求线段 的中点的轨迹方程.
的中点的轨迹方程.
【答案】
(1)椭圆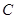 的方程为
的方程为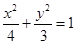 ,焦点为
,焦点为 ;
;
(2) 为所求的轨迹方程.
为所求的轨迹方程.
【解析】
试题分析:解:(1)椭圆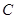 的焦点在
的焦点在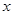 轴上,由椭圆上的点
轴上,由椭圆上的点 到
到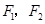 两点的距离之和是4,得
两点的距离之和是4,得 ,即
,即 .
.
又点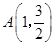 在椭圆上,因此
在椭圆上,因此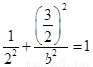 ,
,
得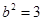 ,且
,且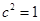 .
.
所以椭圆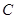 的方程为
的方程为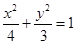 ,焦点为
,焦点为 ;
;
(2)设椭圆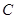 上的动点
上的动点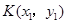 ,线段
,线段 的中点
的中点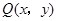 ,满足
,满足 ,
,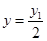 ,
,
即 ,
,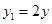 .
.
因此,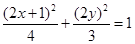 ,即
,即 为所求的轨迹方程.
为所求的轨迹方程.
考点:本题主要考查椭圆的标准方程、几何性质,求轨迹方程的方法。
点评:求椭圆方程,待定系数法是基本方法。相关点法是求轨迹方程的基本方法。

练习册系列答案
相关题目
 分别为椭圆
分别为椭圆 的左、右焦点,点A,B在椭圆上,若
的左、右焦点,点A,B在椭圆上,若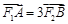 ,
, B.
B. C.
C.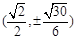 D.
D.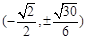
 分别为椭圆
分别为椭圆 的左、右顶点,若在椭圆上存在异于
的左、右顶点,若在椭圆上存在异于 ,使得
,使得 ,其中
,其中 为坐标原点,则椭圆的离心率
为坐标原点,则椭圆的离心率 的取值范围是
的取值范围是  B.
B. C.
C.
 D.
D.
 ,
, 分别为椭圆
分别为椭圆
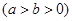 的左、右焦点,过
的左、右焦点,过 与椭圆
与椭圆 相交于
相交于 ,
, 两点,直线
两点,直线 ,
, .
. ,求椭圆
,求椭圆 分别为椭圆
分别为椭圆 的左、右焦点,点
的左、右焦点,点 在椭圆上,若
在椭圆上,若 ;则点
;则点 的坐标是
______.
的坐标是
______. 分别为椭圆
分别为椭圆 的左、右顶点,椭圆长半轴的长等于焦距,且
的左、右顶点,椭圆长半轴的长等于焦距,且 为它的右准线.
为它的右准线. 为右准线上不同于点(4,0)的任意一点,若直线
为右准线上不同于点(4,0)的任意一点,若直线 分别与椭圆相交于异于
分别与椭圆相交于异于 ,证明点
,证明点 在以
在以 为直径的圆内.
为直径的圆内.