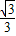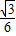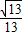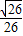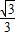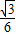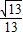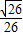题目内容
若底面边长为a的正四棱锥的全面积与棱长为a的正方体的全面积相等,那么这个正四棱锥的侧棱与底面所成角的余弦值为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
分析:求出正方体的表面积,转化为正四棱锥的侧面积,求出棱锥的侧棱长,即可求出正四棱锥的侧棱与底面所成角的余弦值.
解答:解:正方体面积为6a2,四棱锥底面面积为a2,所以四个侧面积为5a2,所以一个侧面面积为1.25a2,由于下边为a,所以侧面三角形的高为2.5a,侧棱长为:
a
这个正四棱锥的侧棱与底面所成角的余弦值:
=
故选C
| ||
| 2 |
这个正四棱锥的侧棱与底面所成角的余弦值:
| ||||
|
| ||
| 13 |
故选C
点评:本题是中档题,考查直线与平面所成角余弦值的求法,考查空间想象能力,计算能力,熟练掌握基本定理、基本方法是解决本题的关键.

练习册系列答案
相关题目