题目内容
【题目】如图所示,在长方体ABCD﹣A1B1C1D1中,AB=5,AD=8,AA1=4,M为B1C1上一点且B1M=2,点N在线段A1D上,A1D⊥AN. 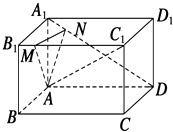
(1)求直线A1D与AM所成角的余弦值;
(2)求直线AD与平面ANM所成角的余弦值.
【答案】
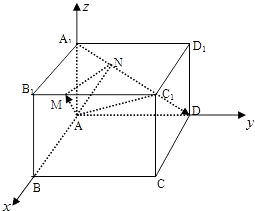
(1)解:建立空间直角坐标系如图.
可得 ![]() =(5,2,4),
=(5,2,4), ![]() =(0,8,﹣4),
=(0,8,﹣4),
∴ ![]()
![]() =(=0+16﹣16=0
=(=0+16﹣16=0
∴ ![]() ⊥
⊥ ![]() ,
,
即直线A1D与AM所成角的余弦值为0
(2)解: ![]() ⊥AM,
⊥AM, ![]() ⊥AN,∴
⊥AN,∴ ![]() ⊥平面AMN,
⊥平面AMN,
∴ ![]() =(0,8,﹣4)是平面AMN的一个法向量,
=(0,8,﹣4)是平面AMN的一个法向量,
又 ![]() =(0,8,0),|
=(0,8,0),| ![]() |=4
|=4 ![]() ,
,
| ![]() |=8,
|=8, ![]()
![]() =64;
=64;
∴cos< ![]() ,
, ![]() >=
>= ![]() =
= ![]() ,
,
∴AD与平面AMN所成的角余弦值为 ![]()
【解析】(1)建立空间直角坐标系,写出两个向量的坐标,利用向量的数量积公式求出两个向量的夹角的余弦.(2)利用线面垂直的判断定理得到 ![]() ⊥平面AMN,利用向量的数量积公式求出法向量
⊥平面AMN,利用向量的数量积公式求出法向量 ![]() 与
与 ![]() 所成角的余弦.
所成角的余弦.
【考点精析】解答此题的关键在于理解异面直线及其所成的角的相关知识,掌握异面直线所成角的求法:1、平移法:在异面直线中的一条直线中选择一特殊点,作另一条的平行线;2、补形法:把空间图形补成熟悉的或完整的几何体,如正方体、平行六面体、长方体等,其目的在于容易发现两条异面直线间的关系,以及对空间角的异直线所成的角的理解,了解已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则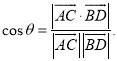 .
.

 阅读快车系列答案
阅读快车系列答案【题目】某职称晋级评定机构对参加某次专业技术考试的100人的成绩进行了统计,绘制了频率分布直方图(如图所示),规定80分及以上者晋级成功,否则晋级失败(满分为100分).


(1)求图中![]() 的值;
的值;
(2)估计该次考试的平均分![]() (同一组中的数据用该组的区间中点值代表);
(同一组中的数据用该组的区间中点值代表);
(3)根据已知条件完成下面![]() 列联表,并判断能否有85%的把握认为“晋级成功”与性别有关?
列联表,并判断能否有85%的把握认为“晋级成功”与性别有关?
(参考公式:  ,其中
,其中![]() )
)
| 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| 0.780 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |