题目内容
设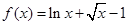 ,证明:
,证明:
(Ⅰ)当x﹥1时,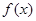 ﹤
﹤ 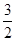 (
( 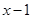 );
);
(Ⅱ)当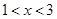 时,
时,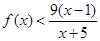 。
。
【答案】
见解析
【解析】(Ⅰ)证法一:记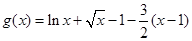 ,
,
则当x>1时,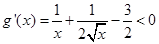 .
.
又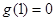 有
有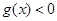 , 即
, 即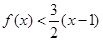
证法二:由均值不等式,当x>1时,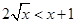 ,故
,故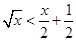 ①
①
令 ,则
,则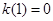 ,
,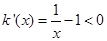 .
.
故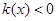 ,即
,即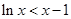 ②
②
由①②得,当x>1时,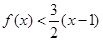 .
.
(Ⅱ)(证法一)
记 ,
,
由(Ⅰ)得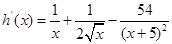


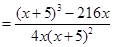
令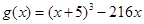 ,
,
则当1<x<3时,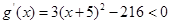
因此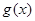 在(1,3)内是递减函数,
在(1,3)内是递减函数,
又由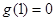 ,得
,得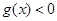 ,
,
所以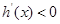
因此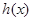 在(1,3)内是递减函数,
在(1,3)内是递减函数,
又由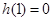 ,得
,得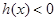 .
.
于是,当1<x<3时,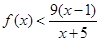
(证法二):
记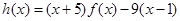
则当1<x<3时,由(Ⅰ)得

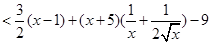
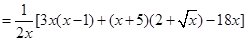
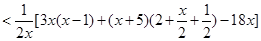

因此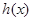 在(1,3)内单调递减
在(1,3)内单调递减
又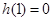 ,所以
,所以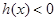 即
即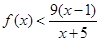 .
.
考点定位:本大题考查导数题目中较为常规的类型题目,考查的切线,单调性,以及最值问题都是课本中要求的重点内容,考查构造函数用求导的方法求最值的能力

练习册系列答案
相关题目
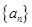 的前
的前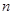 项和为
项和为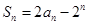 ,
,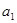 ,
,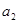 ;
;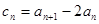 ,证明:数列
,证明:数列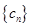 是等比数列;
是等比数列;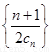 的前
的前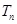 .
.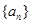 与
与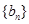 满足:
满足: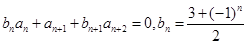 ,
, 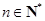 ,且
,且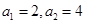 .
.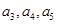 的值;
的值;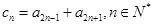 ,证明:
,证明: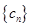 是等比数列;
是等比数列;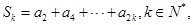 证明:
证明: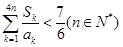 .
. 中,
中,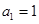 ,
,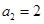 ,且
,且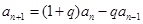
 .
.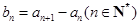 ,证明
,证明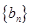 是等比数列;
是等比数列;