题目内容
一般地,如果函数f(x)的图象关于点(a,b)对称,那么对定义域内的任意x,则f(x)+f(2a-x)=2b恒成立.已知函数f(x)=
的定义域为R,其图象关于点M(
,
)对称.
(1)求常数m的值;
(2)解方程:log2[1-f(x)]log2[4-xf(x)]=2;
(3)求证:f(
)+f(
)+…+f(
)+f(
)+f(
)=
(n∈N+).
| 4x |
| 4x+m |
| 1 |
| 2 |
| 1 |
| 2 |
(1)求常数m的值;
(2)解方程:log2[1-f(x)]log2[4-xf(x)]=2;
(3)求证:f(
| 1 |
| n |
| 2 |
| n |
| n-2 |
| n |
| n-1 |
| n |
| n |
| n |
| 3n+1 |
| 6 |
分析:(1)利用函数f(x)=
的图象关于点M(
,
)对称,可得f(x)+f(1-x)=1,代入化简,可得结论;
(2)由(1)知,f(x)=
,代入化简方程,可求方程的解;
(3)利用f(x)+f(1-x)=1,倒序相加,可得结论.
| 4x |
| 4x+m |
| 1 |
| 2 |
| 1 |
| 2 |
(2)由(1)知,f(x)=
| 4x |
| 4x+2 |
(3)利用f(x)+f(1-x)=1,倒序相加,可得结论.
解答:(1)解:∵函数f(x)=
的图象关于点M(
,
)对称,∴f(x)+f(1-x)=1
∴
+
=1
∴
+
=1,∴m=2;
(2)解:由(1)知,f(x)=
∵log2[1-f(x)]log2[4-xf(x)]=2
∴log2(1-
)log2(4-x•
)=2
∴[log2(4x+2)]2-log2(4x+2)-2=0
∴log2(4x+2)=2或log2(4x+2)=-1
∴x=
;
(3)证明:设g(n)=f(
)+f(
)+f(
)+…+f(
)+f(
)可写成g(n)=f(
)+f(
)+f(
)+…+f(
)+f(
)
两式相加,∵f(x)+f(1-x)=1
∴2g(n)=n-1+2f(
)=n-1+2f(1)=
,所以g(n)=
.
| 4x |
| 4x+m |
| 1 |
| 2 |
| 1 |
| 2 |
∴
| 4x |
| 4x+m |
| 41-x |
| 41-x+m |
∴
| 4x |
| 4x+m |
| 4 |
| m•4x+4 |
(2)解:由(1)知,f(x)=
| 4x |
| 4x+2 |
∵log2[1-f(x)]log2[4-xf(x)]=2
∴log2(1-
| 4x |
| 4x+2 |
| 4x |
| 4x+2 |
∴[log2(4x+2)]2-log2(4x+2)-2=0
∴log2(4x+2)=2或log2(4x+2)=-1
∴x=
| 1 |
| 2 |
(3)证明:设g(n)=f(
| 1 |
| n |
| 2 |
| n |
| 3 |
| n |
| n-1 |
| n |
| n |
| n |
| n-1 |
| n |
| n-2 |
| n |
| n-3 |
| n |
| 1 |
| n |
| n |
| n |
两式相加,∵f(x)+f(1-x)=1
∴2g(n)=n-1+2f(
| n |
| n |
| 3n+1 |
| 3 |
| 3n+1 |
| 6 |
点评:本题考查函数的对称性,考查对数方程,考查等式的证明,正确运用函数的对称性是关键.

练习册系列答案
相关题目
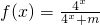 的定义域为R,其图象关于点
的定义域为R,其图象关于点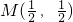 对称.
对称.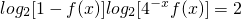 ;
;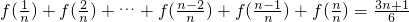 (n∈N+).
(n∈N+).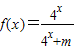 的定义域为R,其图象关于点
的定义域为R,其图象关于点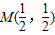 对称.
对称.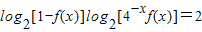 ;
;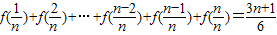 (n∈N+).
(n∈N+).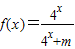 的定义域为R,其图象关于点
的定义域为R,其图象关于点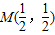 对称.
对称.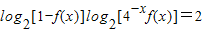 ;
;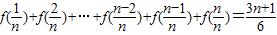 (n∈N+).
(n∈N+).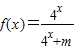 的定义域为R,其图象关于点
的定义域为R,其图象关于点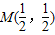 对称.
对称.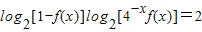 ;
; (n∈N+).
(n∈N+).