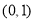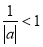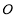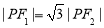题目内容
在平面直角坐标系 中,动点
中,动点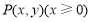 满足:点
满足:点 到定点
到定点 与到
与到 轴的距离之差为
轴的距离之差为 .记动点
.记动点 的轨迹为曲线
的轨迹为曲线 .
.
(1)求曲线 的轨迹方程;
的轨迹方程;
(2)过点 的直线交曲线
的直线交曲线 于
于 、
、 两点,过点
两点,过点 和原点
和原点 的直线交直线
的直线交直线 于点
于点 ,求证:直线
,求证:直线 平行于
平行于 轴.
轴.
(1). 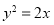 ;(2).详见解析;
;(2).详见解析;
【解析】
试题分析:(1)依题意知,动点 满足:点
满足:点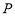 到定点
到定点 与到
与到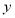 轴的距离之差为
轴的距离之差为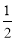 ,由此可得
,由此可得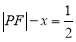 ,进而求曲线C方程;
,进而求曲线C方程;
(2)法Ⅰ:设 ,求出直线
,求出直线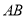 的方程为
的方程为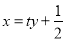 ,将直线与抛物线方程联立
,将直线与抛物线方程联立 得
得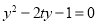 ,得
,得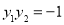 ,求出直线
,求出直线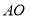 的方程为
的方程为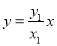 进而点
进而点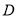 的坐标为
的坐标为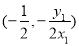
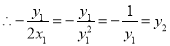
 直线
直线 平行于
平行于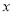 轴;
轴;
法Ⅱ:设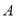 的坐标为
的坐标为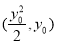 ,求出
,求出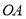 的方程为
的方程为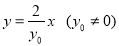 得到点
得到点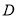 的纵坐标为
的纵坐标为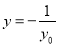 , 由于
, 由于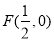 , 则直线
, 则直线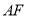 的方程为
的方程为 得点
得点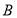 的纵坐标为
的纵坐标为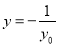 ,则
,则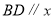 轴;当
轴;当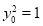 时,结论也成立,故命题得证.
时,结论也成立,故命题得证.
试题解析:(1)依题意: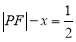 2分
2分
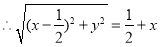
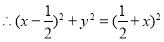 4分
4分
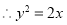 6分
6分
注:或直接用定义求解.
(2)法Ⅰ:设 ,直线
,直线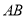 的方程为
的方程为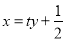
由 得
得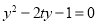 8分
8分
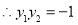
直线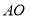 的方程为
的方程为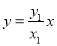
 点
点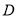 的坐标为
的坐标为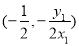 10分
10分
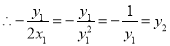
 直线
直线 平行于
平行于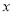 轴. 13分
轴. 13分
法Ⅱ:设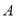 的坐标为
的坐标为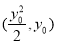 ,则
,则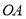 的方程为
的方程为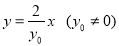
 点
点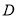 的纵坐标为
的纵坐标为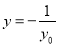 , 8分
, 8分
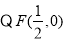
 直线
直线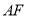 的方程为
的方程为
 点
点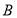 的纵坐标为
的纵坐标为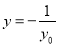 . 11分
. 11分
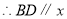 轴;当
轴;当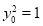 时,结论也成立,
时,结论也成立,
 直线
直线 平行于
平行于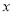 轴. 13分.
轴. 13分.
考点:1. 轨迹方程;2. 直线与圆锥曲线的综合问题.

练习册系列答案
相关题目