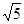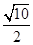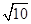题目内容
设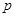 是椭圆
是椭圆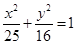 上的点.若
上的点.若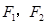 是椭圆的两个焦点,则
是椭圆的两个焦点,则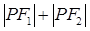 等于( )
等于( )
| A.4 | B.5 | C.8 | D.10 |
D
解析考点:椭圆的简单性质.
专题:计算题.
分析:由椭圆的第一定义知|PF1|+|PF2|=2a,进而求得答案.
解答:解:由椭圆的第一定义知|PF1|+|PF2|=2a=10,
故选D.
点评:本题主要考查了椭圆的性质,属基础题.

练习册系列答案
 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
与椭圆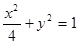 共焦点且过点
共焦点且过点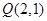 的双曲线方程是
的双曲线方程是
A.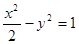 | B.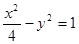 | C.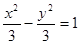 | D.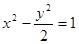 |
抛物线y2=ax(a≠0)的准线方程是 ( )
A.x= -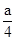 | B.x=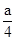 | C.x= -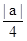 | D.x=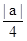 |
设椭圆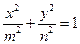 (
(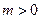 ,
,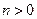 )的右焦点与抛物线
)的右焦点与抛物线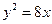 的焦点相同,离心率为
的焦点相同,离心率为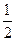 ,则此椭圆的方程为
,则此椭圆的方程为
A.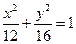 | B.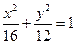 | C. | D.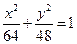 |
已知双 曲线
曲线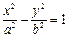 的一个焦点与抛物线
的一个焦点与抛物线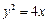 的焦点重合,且双曲线的离心率等于
的焦点重合,且双曲线的离心率等于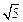 ,则该双曲线的方程为( )
,则该双曲线的方程为( )
A.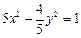 | B.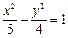 | C.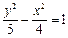 | D.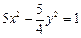 |
抛物线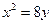 的焦点到准线的距离是
的焦点到准线的距离是
| A. 1 | B. 2 | C. 4 | D. 8 |
双曲线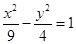 的渐近线方程是
的渐近线方程是
A.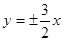 | B.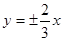 | C.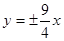 | D.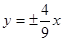 |
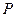 到点
到点 及点
及点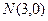 的距离之差为
的距离之差为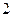 ,则点
,则点 双曲线 B
双曲线 B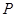 是双曲线
是双曲线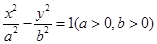 与圆
与圆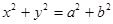 在第一象限的交点,其中
在第一象限的交点,其中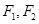 分别是双曲线的左、右焦点,且
分别是双曲线的左、右焦点,且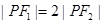 ,则双曲线的离心率为( )
,则双曲线的离心率为( )