题目内容
已知集合A={-2,0,1,3},在平面直角坐标系中,点M的坐标为(x,y),其中x∈A,y∈A。
(1)求点M不在x轴上的概率;
(2)求点M正好落在区域内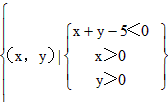 的概率。
的概率。
(1)求点M不在x轴上的概率;
(2)求点M正好落在区域内
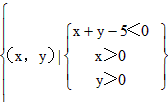 的概率。
的概率。解:(1)∵集合A={-2,0,1,3},x∈A,y∈A,
点M的坐标(x,y)的可能结果是:
(-2,-2),(-2,0),(-2,1),(-2,3);(0,-2),(0,0),(0,1),(0,3);(1,-2),(1,0),(1,1),(1,3);(3,-2),(3,0),(3,1),(3,3),共16种,
点M不在x轴上的坐标共有12种:(-2,-2),(0,-2), (-2,1),(-2,3),(1,-2),(0,1),(1,1),(1,3);(3,-2),(0,3),(3,1),(3,3),
所以点M不在x轴上的概率是 ;
;
(2)点M正好落在区域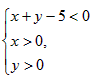 内的坐标共有3种:(1,1),(1,3),(3,1),
内的坐标共有3种:(1,1),(1,3),(3,1),
故点M正好落在该区域内的概率为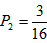 。
。
点M的坐标(x,y)的可能结果是:
(-2,-2),(-2,0),(-2,1),(-2,3);(0,-2),(0,0),(0,1),(0,3);(1,-2),(1,0),(1,1),(1,3);(3,-2),(3,0),(3,1),(3,3),共16种,
点M不在x轴上的坐标共有12种:(-2,-2),(0,-2), (-2,1),(-2,3),(1,-2),(0,1),(1,1),(1,3);(3,-2),(0,3),(3,1),(3,3),
所以点M不在x轴上的概率是
 ;
;(2)点M正好落在区域
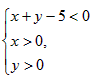 内的坐标共有3种:(1,1),(1,3),(3,1),
内的坐标共有3种:(1,1),(1,3),(3,1),故点M正好落在该区域内的概率为
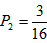 。
。 
练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案
相关题目