题目内容
某单位为普及奥运知识,根据问题的难易程度举办A,B两种形式的知识竞猜活动. A种竞猜活动规定:参赛者回答6个问题后,统计结果,答对4个,可获福娃一个,答对5个或6个,可获其它奖品;B种竞猜活动规定:参赛者依次回答问题,答对一个就结束竞猜且最多可回答6个问题,答对一个问题者可获福娃一个.假定参赛者答对每个题的概率均为 .
.(I)求某人参加A种竞猜活动只获得一个福娃奖品的概率;
(II)设某人参加B种竞猜活动,结束时答题数为η,求Eη.
【答案】分析:(1)参赛者回答6个问题后,统计结果,答对4个,可获福娃一个,依题意答对一题的概率为 ,则根据独立重复试验公式得到结果.
,则根据独立重复试验公式得到结果.
(2)根据题意得到变量的可能取值,根据变量对应的事件,解出概率,写出分布列和期望,在解期望时,这几项的和解题较困难,因此要构造新数列,利用错位相减得到结果.
解答:解:(I)∵参赛者回答6个问题后,统计结果,答对4个,可获福娃一个
设事件“某人参加A种竞猜活动只获得一个福娃奖品”为事件M,
依题意答对一题的概率为 ,则根据独立重复试验公式得到
,则根据独立重复试验公式得到
P(M)=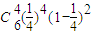
=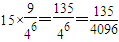 .
.
(II)依题意,某人参加B种竞猜活动,结束时答题数η=1,2,3,4,5,6,
则 ,
,
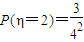 ,
,
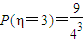 ,
,
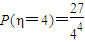 ,
,
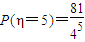 ,
,
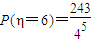 .
.
∴η的分布列是
 ∴
∴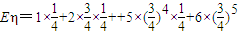
设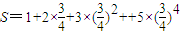 ,
,
则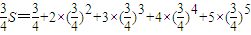
∴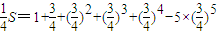 =
=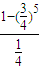
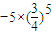 ,
,
∴Eη=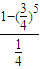
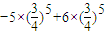 =
=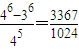 .
.
即某人参加A种竞猜活动只获得一个福娃奖品的概率为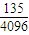 ;
;
某人参加B种竞猜活动,结束时答题数为η,Eη为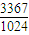 .
.
点评:本题是一个综合问题,考查离散型随机变量的分布列和期望并且结合数列求和的问题,这种类型是近几年高考题中经常出现的,考查离散型随机变量的分布列和期望,大型考试中理科考试必出的一道问题.
 ,则根据独立重复试验公式得到结果.
,则根据独立重复试验公式得到结果.(2)根据题意得到变量的可能取值,根据变量对应的事件,解出概率,写出分布列和期望,在解期望时,这几项的和解题较困难,因此要构造新数列,利用错位相减得到结果.
解答:解:(I)∵参赛者回答6个问题后,统计结果,答对4个,可获福娃一个
设事件“某人参加A种竞猜活动只获得一个福娃奖品”为事件M,
依题意答对一题的概率为
 ,则根据独立重复试验公式得到
,则根据独立重复试验公式得到P(M)=
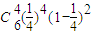
=
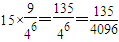 .
.(II)依题意,某人参加B种竞猜活动,结束时答题数η=1,2,3,4,5,6,
则
 ,
,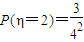 ,
,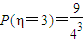 ,
,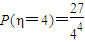 ,
,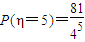 ,
,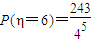 .
.∴η的分布列是
 ∴
∴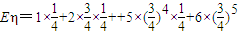
设
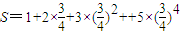 ,
,则
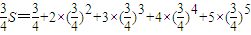
∴
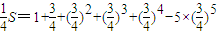 =
=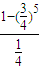
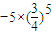 ,
,∴Eη=
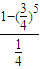
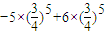 =
=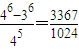 .
.即某人参加A种竞猜活动只获得一个福娃奖品的概率为
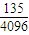 ;
;某人参加B种竞猜活动,结束时答题数为η,Eη为
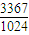 .
.点评:本题是一个综合问题,考查离散型随机变量的分布列和期望并且结合数列求和的问题,这种类型是近几年高考题中经常出现的,考查离散型随机变量的分布列和期望,大型考试中理科考试必出的一道问题.

练习册系列答案
相关题目