题目内容
下列命题中:
①若a,b,m都是正数,且
>
,则b>a;
②已知a,b都为实数,若|a+b|<|a|+|b|,则ab<0;
③若a,b,c为△ABC的三条边,则a2+b2+c2>2(ab+bc+ca);
④若a>b>c,则
+
+
>0.
其中正确命题的个数为( )
①若a,b,m都是正数,且
| a+m |
| b+m |
| a |
| b |
②已知a,b都为实数,若|a+b|<|a|+|b|,则ab<0;
③若a,b,c为△ABC的三条边,则a2+b2+c2>2(ab+bc+ca);
④若a>b>c,则
| 1 |
| a-b |
| 1 |
| b-c |
| 1 |
| c-a |
其中正确命题的个数为( )
| A、1 | B、2 | C、3 | D、4 |
分析:①若a,b,m都是正数,且
>
,则b>a,考查函数f(x)=
的单调性即可;
②已知a,b都为实数,若|a+b|<|a|+|b|,则ab<0,由两数的符号进行判断;
③若a,b,c为△ABC的三条边,则a2+b2+c2>2(ab+bc+ca),利用三角形两这之差小于第三边判断;
④若a>b>c,则
+
+
>0,根据数的取值范围判断.
| a+m |
| b+m |
| a |
| b |
| a+x |
| b+x |
②已知a,b都为实数,若|a+b|<|a|+|b|,则ab<0,由两数的符号进行判断;
③若a,b,c为△ABC的三条边,则a2+b2+c2>2(ab+bc+ca),利用三角形两这之差小于第三边判断;
④若a>b>c,则
| 1 |
| a-b |
| 1 |
| b-c |
| 1 |
| c-a |
解答:解:①若a,b,m都是正数,且
>
,则b>a,考察函数f(x)=
=1+
,由
>
,a,b,m都是正数,知函数f(x)=
是一个增函数,故有a-b<0,此命题正确;
②已知a,b都为实数,若|a+b|<|a|+|b|,则ab<0,由绝对值不等式的意义知,此两数符号相反,故命题正确;
③若a,b,c为△ABC的三条边,则a2+b2+c2>2(ab+bc+ca);三角形中两边之差小于第三边,所以(a-b)2<c2;(b-c)2<a2;(c-a)2<b2;展开后相加整理即可得a2+b2+c2<2(ab+bc+ca),故此命题不对;
④若a>b>c,则
+
+
>0,此命题正确,因为a>b>c,故a-b>0,b-c>0,c-a<0,且b-c+c-a=b-a<0故有
+
>0,即
+
+
>0,成立
综上①②④是正确命题
故选C.
| a+m |
| b+m |
| a |
| b |
| a+x |
| b+x |
| a-b |
| b+x |
| a+m |
| b+m |
| a |
| b |
| a+x |
| b+x |
②已知a,b都为实数,若|a+b|<|a|+|b|,则ab<0,由绝对值不等式的意义知,此两数符号相反,故命题正确;
③若a,b,c为△ABC的三条边,则a2+b2+c2>2(ab+bc+ca);三角形中两边之差小于第三边,所以(a-b)2<c2;(b-c)2<a2;(c-a)2<b2;展开后相加整理即可得a2+b2+c2<2(ab+bc+ca),故此命题不对;
④若a>b>c,则
| 1 |
| a-b |
| 1 |
| b-c |
| 1 |
| c-a |
| 1 |
| b-c |
| 1 |
| c-a |
| 1 |
| a-b |
| 1 |
| b-c |
| 1 |
| c-a |
综上①②④是正确命题
故选C.
点评:本题考查不等关系与不等式,解题的关键是对四个命题涉及的知识熟练掌握,利用不等式的运算规则,通过推理论证判断出命题的大小,本题在验证过程中用到了构造函数的技巧,绝对值不等式的判断,三角形中的关系等,涉及到的知识较多,综合性强,是考查能力的题.题后应好好体会,解题过程中所用的技巧.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目
 ,则
,则 ”的否命题为“若
”的否命题为“若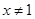 ”
” ”是“
”是“ ”的必要不充分条件
”的必要不充分条件 ,使得
,使得 ”的否定是“
”的否定是“ ,均有
,均有 ”
” 中,若
中,若 ,则
,则 ”的逆否命题为真命题
”的逆否命题为真命题 、β是两个不同的平面,则下列命题中正确的是
、β是两个不同的平面,则下列命题中正确的是 唯一的一个零点同时在区间(0,16),(0,8),(0,4),(0,2)内,那么下列命题中正确的是(
).
唯一的一个零点同时在区间(0,16),(0,8),(0,4),(0,2)内,那么下列命题中正确的是(
).