题目内容
已知平面区域Ω={(x,y)|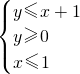 },M={(x,y)|
},M={(x,y)|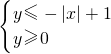 },向区域Ω内随机投一点P,点P落在区域M内的概率为
},向区域Ω内随机投一点P,点P落在区域M内的概率为
- A.

- B.

- C.

- D.

C
分析:本题考查的知识点是线性规划及几何概型的意义,处理的思路为:根据已知的约束条件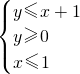 和
和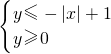 画出满足约束条件的可行域Ω及M的范围,再根据几何概型的意义,求出概率.
画出满足约束条件的可行域Ω及M的范围,再根据几何概型的意义,求出概率.
解答: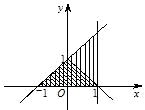 解:如下图,阴影部分大的等腰直角三角形区域为Ω,
解:如下图,阴影部分大的等腰直角三角形区域为Ω,
小的等腰直角三角形区域为M,
由面积比知P= .
.
点评:线性规划与几何概型的综合应用,是高考常见题型,一般以选择或填空的形式出现,解决此类问题的关键是:根据线性规划的约束条件,求出满足条件A的基本事件对应的“几何度量”N(A),再求出总的基本事件对应的“几何度量”N,最后根据P=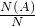 求解.
求解.
分析:本题考查的知识点是线性规划及几何概型的意义,处理的思路为:根据已知的约束条件
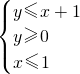 和
和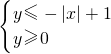 画出满足约束条件的可行域Ω及M的范围,再根据几何概型的意义,求出概率.
画出满足约束条件的可行域Ω及M的范围,再根据几何概型的意义,求出概率.解答:
 解:如下图,阴影部分大的等腰直角三角形区域为Ω,
解:如下图,阴影部分大的等腰直角三角形区域为Ω,小的等腰直角三角形区域为M,
由面积比知P=
 .
.点评:线性规划与几何概型的综合应用,是高考常见题型,一般以选择或填空的形式出现,解决此类问题的关键是:根据线性规划的约束条件,求出满足条件A的基本事件对应的“几何度量”N(A),再求出总的基本事件对应的“几何度量”N,最后根据P=
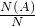 求解.
求解. 
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
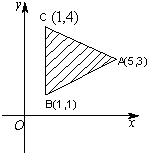 已知平面区域如图所示,z=x+my(m>0)在平面区域内取得最大值时的解(x,y)有无数多个,则m=
已知平面区域如图所示,z=x+my(m>0)在平面区域内取得最大值时的解(x,y)有无数多个,则m=