题目内容

由双曲线=1上的一点P与左、右两焦点F1、F2构成△PF1F2，求△PF1F2的内切圆与边F1F2的切点坐标.

N的坐标为（3，0）


解析:

由双曲线方程知a=3,b=2,c=.

如右图，根据从圆外一点引圆的两条切线长相等及双曲线定义可得

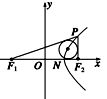|PF1|-|PF2|=2a.

由于|NF1|-|NF2|=|PF1|-|PF2|=2a.                                      ①

|NF1|+|NF2|=2c.                                               ②

由①②得|NF1|==a+c.

∴|ON|=|NF1|-|OF1|=a+c-c=a=3.

故切点N的坐标为（3，0）.

根据对称性，当P在双曲线左支上时，切点N的坐标为（-3，0）.

练习册系列答案
相关题目
已知点P是双曲线
x2
9
-
y2
3
=1右支上任意一点，由P点向两条渐近线引垂直，垂足分别为M、N，则△PMN的面积为
 
．
已知点P是双曲线
x2
9
-
y2
3
=1右支上的任意一点，由P点向双曲线的两条渐近线引垂线，垂足为M和N，则△PMN的面积为（　　）
（2013•浦东新区二模）（1）设椭圆C1：
x2
a2
+
y2
b2
=1与双曲线C2：9x2-
9y2
8
=1有相同的焦点F1、F2，M是椭圆C1与双曲线C2的公共点，且△MF1F2的周长为6，求椭圆C1的方程；
我们把具有公共焦点、公共对称轴的两段圆锥曲线弧合成的封闭曲线称为“盾圆”．
（2）如图，已知“盾圆D”的方程为y2=
4x            (0≤x≤3)
-12(x-4)  (3＜x≤4)
．设“盾圆D”上的任意一点M到F（1，0）的距离为d1，M到直线l：x=3的距离为d2，求证：d1+d2为定值； 
（3）由抛物线弧E1：y2=4x（0≤x≤
2
3
）与第（1）小题椭圆弧E2：
x2
a2
+
y2
b2
=1（
2
3
≤x≤a）所合成的封闭曲线为“盾圆E”．设过点F（1，0）的直线与“盾圆E”交于A、B两点，|FA|=r1，|FB|=r2且∠AFx=α（0≤α≤π），试用cosα表示r1；并求
r1
r2
的取值范围．
（2008•广州二模）（1）椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）与x轴交于A、B两点，点P是椭圆C上异于A、B的任意一点，直线PA、PB分别与y轴交于点M、N，求证：
AN
•
BM
为定值b2-a2．
（2）由（1）类比可得如下真命题：双曲线C：
x2
a2
+
y2
b2
=1（a＞0，b＞0）与x轴交于A、B两点，点P是双曲线C上异于A、B的任意一点，直线PA、PB分别与y轴交于点M、N，则
AN
•
BM
为定值．请写出这个定值（不要求给出解题过程）．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网