题目内容
已知椭圆E: (a>b>0)的左焦点为F,右顶点为A,离心率e=
(a>b>0)的左焦点为F,右顶点为A,离心率e= .
.
(I)若点F在直线l:x-y+1=0上,求椭圆E的方程;
(II)若0<a<1,试探究椭圆E上是否存在点P,使得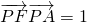 ?若存在,求出点P的个数;若不存在,请说明理由.
?若存在,求出点P的个数;若不存在,请说明理由.
解:(Ⅰ)∵F(-c,0)在直线l:x-y+1=0上,
∴-c+1=0,即c=1,
又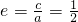 ,∴a=2c=2,
,∴a=2c=2,
∴b=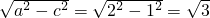 .
.
从而椭圆E的方程为 .
.
(Ⅱ)由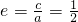 ,得
,得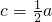 ,
,
∴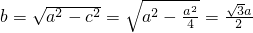 ,
,
椭圆E的方程为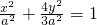 ,其左焦点为
,其左焦点为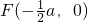 ,右顶点为A(a,0),
,右顶点为A(a,0),
假设椭圆E上存在点P(x0,y0)(-a≤x0≤a),使得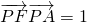 ,
,
∵点P(x0,y0)在椭圆上,∴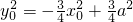 ,
,
由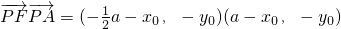
=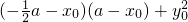
=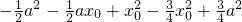
=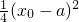 =1.
=1.
解得:x0=a±2,
∵0<a<1,∴
x0=a±2∉[-a,a],
故不存在点P,使得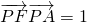 .
.
分析:(Ⅰ)椭圆的左焦点F在直线l:x-y+1=0上,把F的坐标代入直线方程可求c的值,与离心率e= 联立后可求a的值,则椭圆E的方程可求;
联立后可求a的值,则椭圆E的方程可求;
(Ⅱ)假设椭圆E上存在点P,使得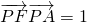 ,设出P点坐标,求出向量
,设出P点坐标,求出向量 和
和 ,代入
,代入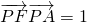 后求出点P的横坐标,由题目给出的a的范围推出点P横坐标不在[-a,a]内,从而得出矛盾,假设错误.
后求出点P的横坐标,由题目给出的a的范围推出点P横坐标不在[-a,a]内,从而得出矛盾,假设错误.
点评:本题考查了直线与圆锥曲线的关系,考查了椭圆的标准方程,训练了存在性问题的处理方法,对于存在性问题,解决的思路是假设结论成立,把假设作为已知条件进行推理,得出正确的等式关系则假设成立,肯定结论,否则假设不成立,否定结论.此题是中档题.
∴-c+1=0,即c=1,
又
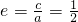 ,∴a=2c=2,
,∴a=2c=2,∴b=
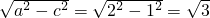 .
.从而椭圆E的方程为
 .
.(Ⅱ)由
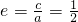 ,得
,得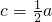 ,
,∴
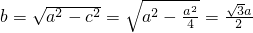 ,
,椭圆E的方程为
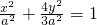 ,其左焦点为
,其左焦点为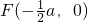 ,右顶点为A(a,0),
,右顶点为A(a,0),假设椭圆E上存在点P(x0,y0)(-a≤x0≤a),使得
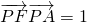 ,
,∵点P(x0,y0)在椭圆上,∴
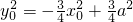 ,
,由
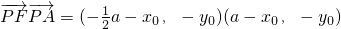
=
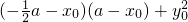
=
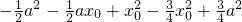
=
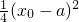 =1.
=1.解得:x0=a±2,
∵0<a<1,∴
x0=a±2∉[-a,a],
故不存在点P,使得
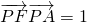 .
.分析:(Ⅰ)椭圆的左焦点F在直线l:x-y+1=0上,把F的坐标代入直线方程可求c的值,与离心率e=
 联立后可求a的值,则椭圆E的方程可求;
联立后可求a的值,则椭圆E的方程可求;(Ⅱ)假设椭圆E上存在点P,使得
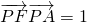 ,设出P点坐标,求出向量
,设出P点坐标,求出向量 和
和 ,代入
,代入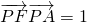 后求出点P的横坐标,由题目给出的a的范围推出点P横坐标不在[-a,a]内,从而得出矛盾,假设错误.
后求出点P的横坐标,由题目给出的a的范围推出点P横坐标不在[-a,a]内,从而得出矛盾,假设错误.点评:本题考查了直线与圆锥曲线的关系,考查了椭圆的标准方程,训练了存在性问题的处理方法,对于存在性问题,解决的思路是假设结论成立,把假设作为已知条件进行推理,得出正确的等式关系则假设成立,肯定结论,否则假设不成立,否定结论.此题是中档题.

练习册系列答案
相关题目
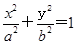 (a>b>0)的离心率e=
(a>b>0)的离心率e=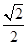 ,左、右焦点分别为F1、F2,点P(2,
,左、右焦点分别为F1、F2,点P(2,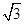 ),点F2在线段PF1的中垂线上
),点F2在线段PF1的中垂线上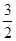 ,0)且互相垂直的两条直线,l1交E于A, B两点,l2交E于C,D两点,求l1的斜率k的取值范围;
,0)且互相垂直的两条直线,l1交E于A, B两点,l2交E于C,D两点,求l1的斜率k的取值范围; ,直线l:x+2y-2=0与x轴,y轴分别交于点A,B.
,直线l:x+2y-2=0与x轴,y轴分别交于点A,B. ,设斜率为k的直线过点F,且与椭圆E相交于M、N两点.
,设斜率为k的直线过点F,且与椭圆E相交于M、N两点. ≤
≤ •
• ≤
≤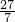 ,求k的取值范围.
,求k的取值范围.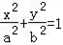 (a>b>0)的右焦点为F(c,0),离心率为
(a>b>0)的右焦点为F(c,0),离心率为 ,A(﹣a,0),
,A(﹣a,0),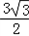 ,设斜率为k的直线过点F,且与椭圆E相交于M、N两点.
,设斜率为k的直线过点F,且与椭圆E相交于M、N两点.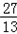 ≤
≤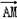 ·
·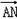 ≤
≤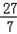 ,求k的取值范围.
,求k的取值范围.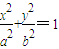 (a>b>0)过点P(3,1),其左、右焦点分别为F1,F2,且
(a>b>0)过点P(3,1),其左、右焦点分别为F1,F2,且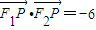 .
.