题目内容
已知椭圆E: (a>b>0)的右焦点为F(c,0),离心率为
(a>b>0)的右焦点为F(c,0),离心率为 ,A(-a,0),B(0,b),且△ABF的面积为
,A(-a,0),B(0,b),且△ABF的面积为 ,设斜率为k的直线过点F,且与椭圆E相交于M、N两点.
,设斜率为k的直线过点F,且与椭圆E相交于M、N两点.
(Ⅰ)求椭圆E的方程;
(Ⅱ)若  ≤
≤ •
• ≤
≤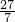 ,求k的取值范围.
,求k的取值范围.
解:(Ⅰ)∵离心率为 ,∴a=2c,b=
,∴a=2c,b= c.
c.
∵△ABF的面积为 ,
,
∴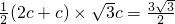 ,∴c=1
,∴c=1
∴a=2,∴
∴椭圆E的方程为 ;
;
(Ⅱ)斜率为k的直线过点F,设方程为y=k(x-1)与 联立,消元可得(3+4k2)x2-8k2x+4k2-12=0
联立,消元可得(3+4k2)x2-8k2x+4k2-12=0
设M(x1,y1),N(x2,y2),则x1+x2=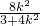 ,
,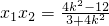
∴y1y2=k2(x1-1)(x2-1)=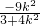
∴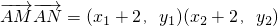 =x1x2+2(x1+x2)+4+y1y2=
=x1x2+2(x1+x2)+4+y1y2=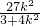
∵ ≤
≤ •
• ≤
≤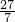 ,∴
,∴ ≤
≤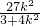 ≤
≤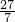
∴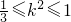
∴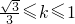 或
或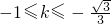
∴k的取值范围是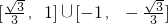 .
.
分析:(Ⅰ)根据椭圆离心率为 ,可得a=2c,b=
,可得a=2c,b= c,利用△ABF的面积为
c,利用△ABF的面积为 ,可求c=1,从而可求椭圆E的方程;
,可求c=1,从而可求椭圆E的方程;
(Ⅱ)设方程为y=k(x-1)与 联立,消元可得(3+4k2)x2-8k2x+4k2-12=0,利用韦达定理,求出
联立,消元可得(3+4k2)x2-8k2x+4k2-12=0,利用韦达定理,求出 •
• ,利用
,利用  ≤
≤ •
• ≤
≤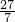 ,即可求得k的取值范围.
,即可求得k的取值范围.
点评:本题考查椭圆的标准方程,考查直线与椭圆的位置关系,考查向量知识的运用,直线与椭圆联立,利用韦达定理是解题的关键.
 ,∴a=2c,b=
,∴a=2c,b= c.
c. ∵△ABF的面积为
 ,
,∴
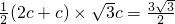 ,∴c=1
,∴c=1∴a=2,∴

∴椭圆E的方程为
 ;
;(Ⅱ)斜率为k的直线过点F,设方程为y=k(x-1)与
 联立,消元可得(3+4k2)x2-8k2x+4k2-12=0
联立,消元可得(3+4k2)x2-8k2x+4k2-12=0设M(x1,y1),N(x2,y2),则x1+x2=
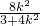 ,
,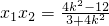
∴y1y2=k2(x1-1)(x2-1)=
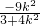
∴
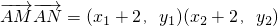 =x1x2+2(x1+x2)+4+y1y2=
=x1x2+2(x1+x2)+4+y1y2=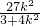
∵
 ≤
≤ •
• ≤
≤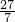 ,∴
,∴ ≤
≤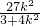 ≤
≤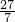
∴
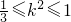
∴
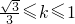 或
或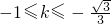
∴k的取值范围是
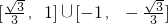 .
.分析:(Ⅰ)根据椭圆离心率为
 ,可得a=2c,b=
,可得a=2c,b= c,利用△ABF的面积为
c,利用△ABF的面积为 ,可求c=1,从而可求椭圆E的方程;
,可求c=1,从而可求椭圆E的方程;(Ⅱ)设方程为y=k(x-1)与
 联立,消元可得(3+4k2)x2-8k2x+4k2-12=0,利用韦达定理,求出
联立,消元可得(3+4k2)x2-8k2x+4k2-12=0,利用韦达定理,求出 •
• ,利用
,利用  ≤
≤ •
• ≤
≤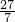 ,即可求得k的取值范围.
,即可求得k的取值范围.点评:本题考查椭圆的标准方程,考查直线与椭圆的位置关系,考查向量知识的运用,直线与椭圆联立,利用韦达定理是解题的关键.

练习册系列答案
 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
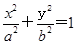 (a>b>0)的离心率e=
(a>b>0)的离心率e=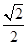 ,左、右焦点分别为F1、F2,点P(2,
,左、右焦点分别为F1、F2,点P(2,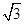 ),点F2在线段PF1的中垂线上
),点F2在线段PF1的中垂线上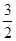 ,0)且互相垂直的两条直线,l1交E于A, B两点,l2交E于C,D两点,求l1的斜率k的取值范围;
,0)且互相垂直的两条直线,l1交E于A, B两点,l2交E于C,D两点,求l1的斜率k的取值范围; ,直线l:x+2y-2=0与x轴,y轴分别交于点A,B.
,直线l:x+2y-2=0与x轴,y轴分别交于点A,B.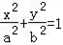 (a>b>0)的右焦点为F(c,0),离心率为
(a>b>0)的右焦点为F(c,0),离心率为 ,A(﹣a,0),
,A(﹣a,0),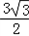 ,设斜率为k的直线过点F,且与椭圆E相交于M、N两点.
,设斜率为k的直线过点F,且与椭圆E相交于M、N两点.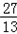 ≤
≤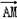 ·
·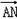 ≤
≤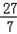 ,求k的取值范围.
,求k的取值范围.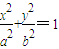 (a>b>0)过点P(3,1),其左、右焦点分别为F1,F2,且
(a>b>0)过点P(3,1),其左、右焦点分别为F1,F2,且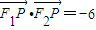 .
.