题目内容
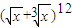的展开式中，含x的正整数次幂的项共有（ ）A．4项
B．3项
C．2项
D．1项
【答案】分析：首先分析题目已知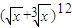
，是含有
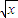和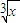
的和的12次幂的形式，求含x的正整数次幂的项的个数．考虑到根据二项式定理的性质，写出
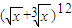的展开式的通项，然后使得x的幂为正整数，即可求出满足条件的个数．
解答：解：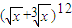
根据二项式定理的性质得：
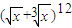的展开式的通项为
，
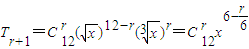故含x的正整数次幂的项即6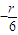
（0≤r≤12）为整数的项，共有3项，即r=0或r=6或r=12．
故选B．
点评：此题主要考查二项式定理的性质问题，其中涉及到二项式展开式的通项的求法，属于基础性试题，在高考中多以选择题、填空题的形式出现，同学们需要掌握．
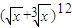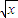，是含有和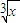的和的12次幂的形式，求含x的正整数次幂的项的个数．考虑到根据二项式定理的性质，写出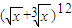的展开式的通项，然后使得x的幂为正整数，即可求出满足条件的个数．解答：解：
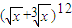根据二项式定理的性质得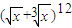：的展开式的通项为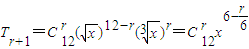，故含x的正整数次幂的项即6
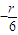（0≤r≤12）为整数的项，共有3项，即r=0或r=6或r=12．故选B．
点评：此题主要考查二项式定理的性质问题，其中涉及到二项式展开式的通项的求法，属于基础性试题，在高考中多以选择题、填空题的形式出现，同学们需要掌握．
练习册系列答案
相关题目
(
+
)12的展开式中，含x的正整数次幂的项共有（ ）
| x |
| 3 | x |
| A、4项 | B、3项 | C、2项 | D、1项 |
)12的展开式中，含x的正整数次幂的项共有( )
的展开式中，含x的正整数次幂的项共有（ ） 
的展开式中，含x的正整数次幂的项共有（ ）