题目内容
已知函数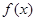 的定义域为
的定义域为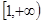 ,且
,且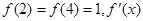 为
为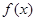 的导函数,函数
的导函数,函数 的图象如图所示.则不等式组
的图象如图所示.则不等式组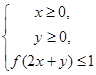 所表示的平面区域的面积是
所表示的平面区域的面积是
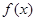 的定义域为
的定义域为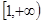 ,且
,且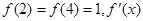 为
为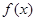 的导函数,函数
的导函数,函数 的图象如图所示.则不等式组
的图象如图所示.则不等式组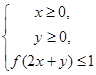 所表示的平面区域的面积是
所表示的平面区域的面积是
A.3 | B.4 | C.5 | D.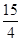 |
A
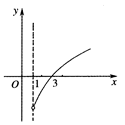
分析:根据函数图象,我们易得到f(x)在[1,3)上是减函数,在[3,+∞)上是增函数,结合f(2)=f(4)=1,我们易构造出一个关于x,y的二元一次不等式组,画出满足条件的可行域,根据平面图象面积公式,我们易得答案.
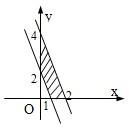
解:由图可知,f(x)在[1,3)上是减函数,
在[3,+∞)上是增函数,
又f(2)=f(4)=1,
f(2x+y)≤1,
所以2≤2x+y≤4,
从而不等式组为,作出可行域如图所示,
其面积为S=×2×4-×1×2=3.
故选A

练习册系列答案
 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
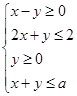 表示的平面区域是一个四边形,则
表示的平面区域是一个四边形,则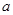 的取值范围是
的取值范围是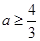
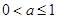
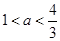
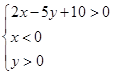 表示的平面区域内的整点坐标是 .
表示的平面区域内的整点坐标是 .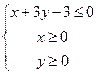 ,则
,则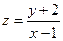 的取值范围是 ▲ .
的取值范围是 ▲ .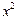 +
+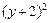 =1上,点M(x,y)在平面区域
=1上,点M(x,y)在平面区域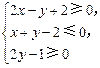 上,则AM的最小值是 .
上,则AM的最小值是 .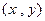 满足
满足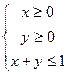 ,则
,则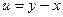 的取值范围是 .
的取值范围是 .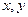 满足
满足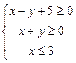 ,则
,则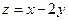 的最小值是 .
的最小值是 . 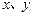 满足
满足 ,则
,则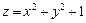 的最小值为________________.
的最小值为________________.