题目内容
某公司生产的A型商品通过租赁柜台进入某商场销售.第一年,商场为吸引厂家,决定免收该年管理费,因此,该年A型商品定价为每件70元,年销售量为11.8万件.第二年,商场开始对该商品征收比率为p%的管理费(即销售100元要征收p元),于是该商品的定价上升为每件![]() 元,预计年销售量将减少p万件.
元,预计年销售量将减少p万件.
(1) 将第二年商场对该商品征收的管理费y(万元)表示成p的函数,并指出这个函数的定义域;
(2) 要使第二年商场在此项经营中收取的管理费不少于14万元,则商场对该商品征收管理费的比率p%的范围是多少?
(3) 第二年,商场在所收管理费不少于14万元的前提下,要让厂家获得最大销售金额,则p应为多少?
解:(1)依题意,第二年该商品年销售量为(11.8-p)万件,
年销售收入为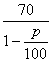 (11.8一p)万元,
(11.8一p)万元,
则商场该年对该商品征收的总管理费为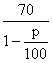 (11?8一p)p%(万元)
(11?8一p)p%(万元)
故所求函数为 y=![]()
由11.8-p>0及p>0得定义域为0<p<11.8
(2) 由y≥14得![]() ≥14
≥14
化简得p2-12p+20≤0,即(p-2)(p-10)≤0,解得2≤p≤l0
故当比率为[2%,10%]内时,商场收取的管理费将不少于14万元.
(3) 第二年,当商场收取的管理费不少于14万元时,
厂家的销售收入为g(p)= ![]() (2≤p≤10)
(2≤p≤10)
∵ g(p)= ![]() =700(10+
=700(10+![]() )为减函数,
)为减函数,
∴ g(p)max =g(2)=700(万元)
故当比率为2%时,厂家销售金额最大,且商场所收管理费又不少于14万元。

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目