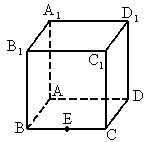
题目内容
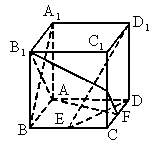
如图所示,在棱长为1的正方体ABCD- 中,点E是棱BC的中点,点F是棱CD上的动点.
中,点E是棱BC的中点,点F是棱CD上的动点.
(1)试确定点F的位置,使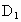 E⊥平面A
E⊥平面A F;
F;
(2)当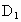 E⊥平面A
E⊥平面A F时,求二面角
F时,求二面角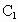 -EF-A的大小(结果用反三角函数值表示).
-EF-A的大小(结果用反三角函数值表示).
答案:略
解析:
解析:
|
本小题主要考查线面关系和正方体等基础知识,考查空间想象能力和推理运算能力. 解: (1)连结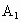 B,∵ B,∵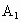  ∥BC, ∥BC,
∴ 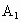 ,B,E, ,B,E, 四点共面,如图所示. 四点共面,如图所示.
在正方形 AB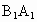 中, 中,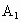 B⊥A B⊥A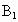 , ,
∵ BE⊥平面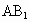 ,A ,A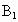 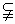 平面A 平面A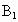 , ,
∴ 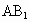 ⊥BE.∵ ⊥BE.∵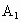 B∩BE=B, B∩BE=B,
∴ 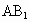 ⊥平面 ⊥平面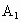 BE BE . .
又  E E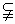 平面 平面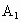 BE BE ,∴ ,∴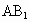 ⊥ ⊥ E. E.
若要使  E⊥平面A E⊥平面A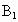 F,则必有 F,则必有 E⊥AF. E⊥AF.
连结 DE,由于 D⊥平面AC,AF D⊥平面AC,AF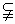 平面AC, 平面AC,
∴  D⊥AF.要有AF⊥ D⊥AF.要有AF⊥ E,∴应有AF⊥DE. E,∴应有AF⊥DE.
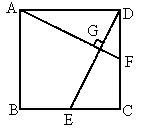
如图所示,由于 E是BC的中点,若要 AF⊥DE,则∠DGF=90°,∵∠ FDG+∠DEC=90°,又必有∠ FDG+∠DFG=90°,从而应有∠ DFG=∠DEC,∴△ ADF≌△DCE,∴F应为DC的中点.∴当 F为DC的中点时, E⊥平面A E⊥平面A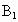 F. F.
(2) 略.把握几何图形特征求解. |

练习册系列答案
相关题目
 如图所示,在棱长为1的正方体ABCD-A1B1C1D1的面对角线A1B上存在一点P使得AP+D1P取得最小值,则此最小值为
如图所示,在棱长为1的正方体ABCD-A1B1C1D1的面对角线A1B上存在一点P使得AP+D1P取得最小值,则此最小值为 一点
一点 的面对角线
的面对角线 上存在一点
上存在一点 使得
使得 最短,则
最短,则
 B.
B. C.
C. D.
D.
 的面对角线
的面对角线 上存在一点
上存在一点 使得
使得 取得最小值,则此最小值为
取得最小值,则此最小值为 
 的面
的面 上存在一点
上存在一点 使得
使得 取得最小值,则此
取得最小值,则此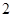 B.
B. C.
C. D.
D.