题目内容
1.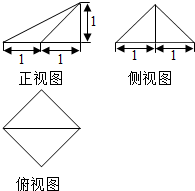 一个四棱锥的三视图如图所示,则该几何体的体积=$\frac{2}{3}$,表面积=2+$\sqrt{2}$+$\sqrt{6}$.
一个四棱锥的三视图如图所示,则该几何体的体积=$\frac{2}{3}$,表面积=2+$\sqrt{2}$+$\sqrt{6}$.
分析 根据四棱锥的三视图,得出该四棱锥是底面为正方形,一条侧棱垂直于底面,
画出图形结合图形即可求出它的体积与表面积.
解答 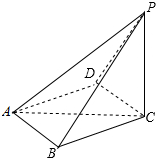 解:根据四棱锥的三视图,得;
解:根据四棱锥的三视图,得;
该四棱锥是底面是对角线为2的正方形,
且一条侧棱垂直于底面,如图所示;
所以,该四棱锥的体积是$\frac{1}{3}$×$\frac{1}{2}$×22×1=$\frac{2}{3}$;
表面积是S△PBC+S△PDC+S△PAB+S△PAD+S正方形ABCD
=$\frac{1}{2}$×$\sqrt{2}$×1+$\frac{1}{2}$×$\sqrt{2}$×1+$\frac{1}{2}$×$\sqrt{2}$×$\sqrt{{(\sqrt{2})}^{2}{+1}^{2}}$+$\frac{1}{2}$×$\sqrt{2}$×$\sqrt{{(\sqrt{2})}^{2}{+1}^{2}}$+$\frac{1}{2}$×22=$\sqrt{2}$+$\sqrt{6}$+2.
故答案为:$\frac{2}{3}$,2+$\sqrt{2}$+$\sqrt{6}$.
点评 本题考查了由三视图求几何体的表面积与体积的应用问题,解题的关键是判断几何体的形状,是基础题目.

练习册系列答案
相关题目
9.一个金鱼缸,现已注满水.有大、中、小三个假山,第一次把小假山沉入水中,第二次把小假山取出,把中假山沉入水中,第三次把中假山取出,把小假山和大假山一起沉入水中,现知道每次溢出水量的情况是:第一次是第二次的$\frac{1}{3}$.第三次是第二次的2倍,问三个假山体积之比( )
| A. | 1:3:5 | B. | 1:4:9 | C. | 3:6:7 | D. | 6:7:8 |
6.等差数列{an}的前n项和为Sn,若当首项a1和公差d变化时,a3+a10+a11是一个定值,则下列选项中为定值的是( )
| A. | S17 | B. | S16 | C. | S15 | D. | S14 |
11.设非零向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为θ,则θ∈($\frac{π}{2}$,π)是$\overrightarrow{a}$•$\overrightarrow{b}$<0的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
 如图,在圆柱EF中,底面圆的半径为2,母线长为6,$\widehat{AB}$和$\widehat{CD}$的长均为所在圆的周长的$\frac{1}{6}$,若沿着面ABCD将圆柱截开,试求所截得的体积较小的几何体的体积V.
如图,在圆柱EF中,底面圆的半径为2,母线长为6,$\widehat{AB}$和$\widehat{CD}$的长均为所在圆的周长的$\frac{1}{6}$,若沿着面ABCD将圆柱截开,试求所截得的体积较小的几何体的体积V.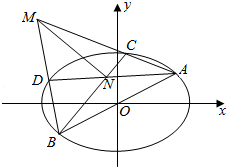 如图,在平面直角坐标系xoy中,椭圆E:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{{\sqrt{2}}}{2}$,直线l:y=$\frac{1}{2}$x与椭圆E相交于A,B两点,AB=$4\sqrt{5}$,C,D是椭圆E上异于A,B两点,且直线AC,BD相交于点M,直线AD,BC相交于点N.
如图,在平面直角坐标系xoy中,椭圆E:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{{\sqrt{2}}}{2}$,直线l:y=$\frac{1}{2}$x与椭圆E相交于A,B两点,AB=$4\sqrt{5}$,C,D是椭圆E上异于A,B两点,且直线AC,BD相交于点M,直线AD,BC相交于点N.