题目内容
 和
和 是表示平面内所有向量的一组基底,则下面的四个向量中,不能作为一组基底的是( )
是表示平面内所有向量的一组基底,则下面的四个向量中,不能作为一组基底的是( )A.3
 -2
-2 和4
和4 -6
-6
B.
 +
+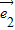 和
和 -
-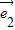
C.
 +2
+2 和
和 +2
+2
D.
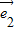 和
和 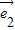 +
+
【答案】分析:由题意,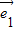 和
和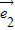 是表示平面内所有向量的一组基底,找出不能作为一组基底的向量方法就是验证它们共线,故对四个选项进行考查,找出共线的那一组即可找到正确选项
是表示平面内所有向量的一组基底,找出不能作为一组基底的向量方法就是验证它们共线,故对四个选项进行考查,找出共线的那一组即可找到正确选项
解答:解:由题意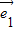 和
和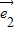 是表示平面内所有向量的一组基底,
是表示平面内所有向量的一组基底,
A选项中,存在一个实数-2使得4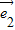 -6
-6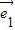 =-2(3
=-2(3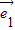 -2
-2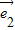 ),此两向量共线,故不能作为基底,A可选;
),此两向量共线,故不能作为基底,A可选;
B选项中找不到一个非零实数λ使得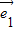 +
+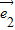 =λ(
=λ(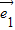 -
-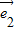 )成立,故不能选B;
)成立,故不能选B;
C选项与D选项中的两个向量是不共线的,可以作为一组基底,
综上,A选项中的两个向量不能作为基底.
故选A.
点评:本题考查平面向量的基本定理中基底的意义,解题的关键是理解基底中的两个基向量是不共线的,本题的难点是验证向量的共线,对基底的考查是近几年高考的热点,题后要注意总结做题规律
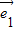 和
和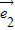 是表示平面内所有向量的一组基底,找出不能作为一组基底的向量方法就是验证它们共线,故对四个选项进行考查,找出共线的那一组即可找到正确选项
是表示平面内所有向量的一组基底,找出不能作为一组基底的向量方法就是验证它们共线,故对四个选项进行考查,找出共线的那一组即可找到正确选项解答:解:由题意
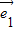 和
和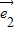 是表示平面内所有向量的一组基底,
是表示平面内所有向量的一组基底,A选项中,存在一个实数-2使得4
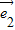 -6
-6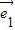 =-2(3
=-2(3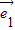 -2
-2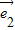 ),此两向量共线,故不能作为基底,A可选;
),此两向量共线,故不能作为基底,A可选;B选项中找不到一个非零实数λ使得
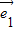 +
+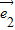 =λ(
=λ(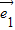 -
-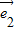 )成立,故不能选B;
)成立,故不能选B;C选项与D选项中的两个向量是不共线的,可以作为一组基底,
综上,A选项中的两个向量不能作为基底.
故选A.
点评:本题考查平面向量的基本定理中基底的意义,解题的关键是理解基底中的两个基向量是不共线的,本题的难点是验证向量的共线,对基底的考查是近几年高考的热点,题后要注意总结做题规律

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
 和
和 是表示平面内所有向量的一组基底,则下面的四个向量中,不能作为一组基底的是 ________
是表示平面内所有向量的一组基底,则下面的四个向量中,不能作为一组基底的是 ________