题目内容
如图(1)所示,⊙O的直径AB=4,点C,D为⊙O上两点,且∠CAB=45°,∠DAB=60°,F为 的中点.沿直径AB折起,使两个半圆所在平面互相垂直(如图(2)所示).
的中点.沿直径AB折起,使两个半圆所在平面互相垂直(如图(2)所示).

(1)求证:OF∥平面ACD;
(2)在 上是否存在点G,使得FG∥平面ACD?若存在,试指出点G的位置,并求点G到平面ACD的距离;若不存在,请说明理由.
上是否存在点G,使得FG∥平面ACD?若存在,试指出点G的位置,并求点G到平面ACD的距离;若不存在,请说明理由.
(1)见解析(2)存在,h=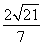
【解析】(1)证明:如图所示,联结CO,

∵∠CAB=45°,∴CO⊥AB,
又∵F为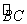 的中点,∴∠FOB=45°,
的中点,∴∠FOB=45°,
∴OF∥AC.
∵OF平面ACD,AC平面ACD,
∴OF∥平面ACD.
(2)设在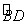 上存在点G,使得FG∥平面ACD,联结OG,如图.
上存在点G,使得FG∥平面ACD,联结OG,如图.
∵OF∥平面ACD,OF∩FG=F,∴平面OFG∥平面ACD,
∴OG∥AD,∠BOG=∠BAD=60°.
因此,在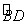 上存在点G,使得FG∥平面ACD,且点G为
上存在点G,使得FG∥平面ACD,且点G为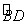 的中点.
的中点.
联结AG,过C作CE⊥AD于E,联结OE,设点G到平面ACD的距离为h.
∵S△ACD= ·AD·CE=
·AD·CE=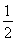 ×2×
×2× =
=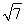 ,S△GAD=S△OAD=
,S△GAD=S△OAD=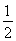 ×2×
×2×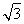 =
= ,
,
∴由V三棱锥G-ACD=V三棱锥C-AGD,得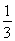 ×
×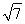 ×h=
×h=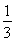 ×
× ×2,则h=
×2,则h=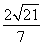 .
.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目





