题目内容
函数y=3sin (x∈[0,π])的单调递增区间是( )
(x∈[0,π])的单调递增区间是( )
A. | B. |
C. | D. |
B
解析试题分析:由 得,
得, ,所以
,所以 是函数y=3sin
是函数y=3sin (x∈[0,π])的单调递增区间,故选B。
(x∈[0,π])的单调递增区间,故选B。
考点:本题主要考查正弦型函数的图象和性质。
点评:易错题,复合函数的单调性判断,遵循“内外层函数,‘同增异减’”。

练习册系列答案
相关题目
设 是定义在
是定义在 上的周期函数,周期为
上的周期函数,周期为 ,对
,对 都有
都有 ,且当
,且当 时,
时, ,若在区间
,若在区间 内关于
内关于 的方程
的方程 =0
=0 恰有3个不同的实根,则
恰有3个不同的实根,则 的取值范围是
的取值范围是
| A.(1,2) | B. | C. | D. |
将函数y=sin(x- )的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再将所得的图象向左平移
)的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再将所得的图象向左平移 个单位,得到的图象对应的解析式是 ( )
个单位,得到的图象对应的解析式是 ( )
A.y=sin x x | B.y=sin( x- x- ) ) | C.y=sin( x- x- ) ) | D.y=sin(2x- ) ) |
已知点P( )在第三象限,则角
)在第三象限,则角 是( )
是( )
| A.第一象限角 | B.第二象限角 | C.第三象限角 | D.第四象限角 |
函数y=sin (2x+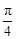 )的图象可由函数y=sin 2x的图象
)的图象可由函数y=sin 2x的图象
A.向左平移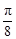 个单位长度而得到 个单位长度而得到 | B.向右平移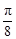 个单位长度而得到 个单位长度而得到 |
C.向左平移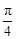 个单位长度而得到 个单位长度而得到 | D.向右平移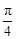 个单位长度而得到 个单位长度而得到 |
若 ,则tan
,则tan =
=
A. | B. | C. | D. |
使函数
 为增函数的区间是( )
为增函数的区间是( )
A. | B. | C. | D. |
在同一平面直角坐标系中,画出三个函数 ,
, ,
, 的部分图象(如图),则( )
的部分图象(如图),则( )
A. 为 为 , , 为 为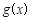 , , 为 为 |
B. 为 为 , , 为 为 , , 为 为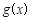 |
C. 为 为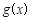 , , 为 为 , , 为 为 |
D. 为 为 , , 为 为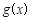 , , 为 为 |
 )+
)+ 是奇函数,且在[0,
是奇函数,且在[0, 上是减函数的
上是减函数的


