题目内容
已知等差数列{an}的首项为a,公差为b;等比数列{bn}的首项为b,公比为a,其中a,b∈N+,且a1<b1<a2<b2<a3.
(1)求a的值;
(2)若对于任意n∈N+,总存在m∈N+,使am+3=bn,求b的值;
(3)在(2)中,记{cn}是{an}中所有满足am+3=bn的项从小到大依次组成的数列,又记Sn为{cn}的前n项和,Tn为{an}的前n项和,求证:Sn≥Tn(n∈N+).
答案:
解析:
解析:
|
解:(1)∵ ∴ ∴a=2或a=3 当a=3时, ∴a=2. 4分; (2) ∴ ∴b=5 8分; (3)由(2)知 ∴ ∴ ∵ 当n≥3时, ∴ 综上得 |

练习册系列答案
相关题目
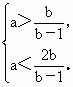 ∴
∴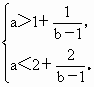 ∴
∴ 已知等差数列{an}中,a4a6=-4,a2+a8=0,n∈N*.
已知等差数列{an}中,a4a6=-4,a2+a8=0,n∈N*.