题目内容
(本小题13分)已知椭圆![]() ,长轴长是
,长轴长是![]() ,离心率是
,离心率是![]() .
.
(Ⅰ)求椭圆的方程;
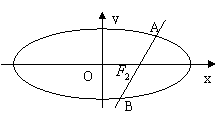
(Ⅱ)过椭圆右焦点![]() 的直线与椭圆相交于
的直线与椭圆相交于![]() 两点,在
两点,在![]() 轴上是否存在定点
轴上是否存在定点![]() ,使
,使![]() 为常数?若存在,求出定点
为常数?若存在,求出定点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
 |
 (本小题13分)解析:(Ⅰ)
(本小题13分)解析:(Ⅰ)![]() ------------5分
------------5分
(Ⅱ)当![]() 不与
不与![]() 轴垂直时,设过点
轴垂直时,设过点![]() 的直线
的直线
 |
并设![]() ,由
,由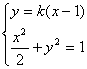
消去![]() 得
得
![]()
![]() --------8分
--------8分
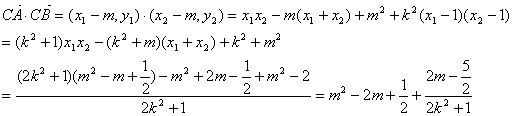
![]() 是与
是与![]() 无关的常数,所以
无关的常数,所以![]() 即
即![]() ,此时
,此时![]() --10分
--10分
当![]() 与
与![]() 轴垂直时,点
轴垂直时,点![]() 的坐标分别是
的坐标分别是![]() ,
,
此时![]() .-----12分
.-----12分
综上所述,在![]() 轴上存在定点
轴上存在定点![]() ,使
,使![]() 为常数
为常数![]() .------------13分
.------------13分

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
 ,
,
 ∥
∥ 时,求
时,求 的值;
的值; 在
在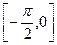 上的值域.
上的值域. 满足
满足 ,且
,且 是
是 ,
, 的等差中项.
的等差中项. ,
, ,求使
,求使
 成立的正整数
成立的正整数 的最小值.
的最小值. 过直线
过直线 和
和 的交点;
的交点;  垂直,求直线
垂直,求直线 到直线
到直线 的距离为1.求直线
的距离为1.求直线 ,过
,过 作直线
作直线 .
.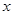 轴不垂直,交抛物线于A、B两点,是否存在
轴不垂直,交抛物线于A、B两点,是否存在 ,使得
,使得 ?若存在,求出m的值;若不存在,请说明理由?
?若存在,求出m的值;若不存在,请说明理由? 轴和
轴和 为定值,试证之;
为定值,试证之;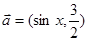 ,
,
 ∥
∥ 时,求
时,求 的值;
的值;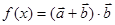 在
在 上的值域.
上的值域.