题目内容
已知数列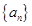 中,
中,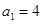 ,
,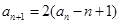 ,(1)求证:数列
,(1)求证:数列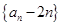 为等比数列。(2)设数列
为等比数列。(2)设数列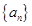 的前
的前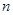 项和为
项和为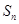 ,若
,若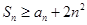 ,求正整数列
,求正整数列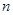 的最小值。
的最小值。
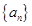 中,
中,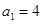 ,
,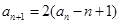 ,(1)求证:数列
,(1)求证:数列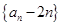 为等比数列。(2)设数列
为等比数列。(2)设数列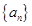 的前
的前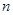 项和为
项和为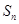 ,若
,若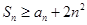 ,求正整数列
,求正整数列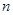 的最小值。
的最小值。(1)见解析;(2)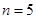 .
.
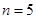 .
.本试题主要是考查了通项公式的求解和数列的不等式的证明问题的综合运用
(1)利用递推关系可知,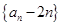 为等比数列,从而得到结论。
为等比数列,从而得到结论。
(2)结合上一问的结论可知,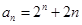 ,和
,和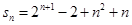 ,然后解不等式得到n的取值。
,然后解不等式得到n的取值。
解:因为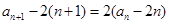
所以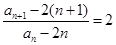
所以数列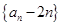 为等比数列。
为等比数列。
(2)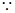

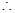
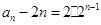
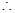
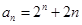
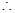
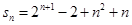
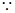
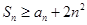 可知
可知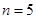 时满足条件。
时满足条件。
(1)利用递推关系可知,
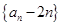 为等比数列,从而得到结论。
为等比数列,从而得到结论。(2)结合上一问的结论可知,
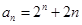 ,和
,和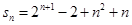 ,然后解不等式得到n的取值。
,然后解不等式得到n的取值。解:因为
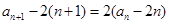
所以
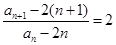
所以数列
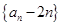 为等比数列。
为等比数列。(2)
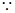

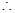
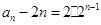
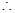
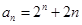
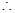
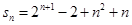
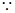
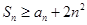 可知
可知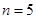 时满足条件。
时满足条件。
练习册系列答案
 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
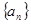 的前三项依次为a-1,a+1,a+4,则此数列的通项公式为( )
的前三项依次为a-1,a+1,a+4,则此数列的通项公式为( )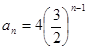
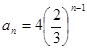
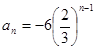
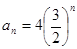
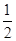 ,a3+a4=1,则a7+a8+a9+a10=_____
,a3+a4=1,则a7+a8+a9+a10=_____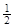 为公比的等比数列,体积分别记为
为公比的等比数列,体积分别记为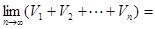 .
. 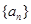 的首项为
的首项为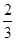 ,且
,且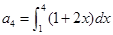 ,则公比等于 。
,则公比等于 。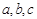 成等比数列,且满足
成等比数列,且满足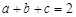 ,则实数
,则实数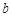 的取值范围为________.
的取值范围为________.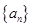 中,
中,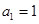 对所有的
对所有的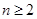 都有
都有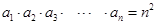 ,则
,则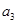 的值为( )
的值为( )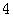
 前
前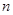 项的和为
项的和为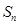 , 若
, 若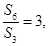 则
则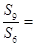 ( )
( )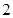


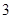
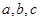 成等比数列,且
成等比数列,且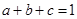 ,则
,则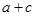 的取值范围是 .
的取值范围是 .