题目内容
直线tx+y-t+1=0(t∈R)与圆x2+y2-2x+4y-4=0的位置关系为( )
| A.相交 | B.相切 | C.相离 | D.以上都有可能 |
A
解析

练习册系列答案
相关题目
已知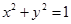 ,则
,则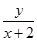 的取值范围是( )
的取值范围是( )
A.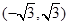 | B.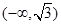 | C.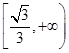 | D.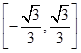 |
已知 为圆
为圆 的两条互相垂直的弦,且垂足为
的两条互相垂直的弦,且垂足为 ,则四边形
,则四边形 面积的最大值为( )
面积的最大值为( )
| A.5 | B.10 | C.15 | D.20 |
直线 :
: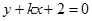 与曲线C:
与曲线C: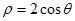 有交点,则
有交点,则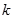 的取值范围是( )
的取值范围是( )
A.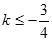 | B.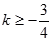 | C.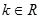 | D.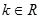 但 但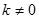 |
已知圆C:x2+(y-3)2=4,过A(-1,0)的直线l与圆C相交于P,Q两点,若|PQ|=2 ,则直线l的方程为( )
,则直线l的方程为( )
| A.x=-1或4x+3y-4=0 |
| B.x=-1或4x-3y+4=0 |
| C.x=1或4x-3y+4=0 |
| D.x=1或4x+3y-4=0 |
已知圆C:x2+y2+mx-4=0上存在两点关于直线x-y+3=0对称,则实数m的值为( )
| A.8 | B.-4 | C.6 | D.无法确定 |
若圆O:x2+y2=4与圆C:x2+y2+4x-4y+4=0关于直线l对称,则直线l的方程是( )
| A.x+y=0 | B.x-y=0 |
| C.x-y+2=0 | D.x+y+2=0 |
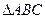 的顶点A为(3,-1),AB边上的中线所在直线方程为
的顶点A为(3,-1),AB边上的中线所在直线方程为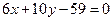 ,
,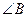 的平分线所在直线方程为
的平分线所在直线方程为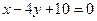 ,求BC边所在直线的方程.
,求BC边所在直线的方程.