题目内容
设a,b,c是实数(a<b),m,n,p是正实数,函数f(x)=(x-a)(x-b);(1)证明方程f(x)=p有两个不等实数根;
(2)设(1)中的方程的两根为α、β(α<β),试确定α、β、a、b四个数的大小关系;
(3)设g(x)=f(x)(x-c)-(m+n+p)x+(am+bn+cp),对于(2)中的α、β请判断g(α)及g(β)的符号.
【答案】分析:(1)证明方程f(x)=p有两个不等实数根,只需要证明方程根的判别式大于0即可;
(2)方程f(x)=p的两根为α、β(α<β),即y=f(x)与y=p的图象交点的横坐标为α、β,又y=f(x)与y=0的图象交点的横坐标为a,b(a>b),且y=f(x)的图象开口向上,从而可得结论;
(3)由题意,(α-a)(α-b)=p,g(α)=(a-α)m+(b-α)n,根据a>α,b>α,m>0,n>0,可得g(α)>0;同理g(β)=(a-β)m+(b-β)n,根据a<β,b<β,m>0,n>0,可得g(β)<0.
解答:(1)证明:由f(x)=p,可化为x2+(a+b)x+ab-p=0
∵△=(a+b)2-4(ab-p)=(a-b)2+4p,p>0
∴△>0
故方程f(x)=p有两个不等实数根
( 2)解:方程f(x)=p的两根为α、β(α<β),即y=f(x)与y=p的图象交点的横坐标为α、β,又y=f(x)与y=0的图象交点的横坐标为a,b(a>b),且y=f(x)的图象开口向上,如图所示,可知α<a<b<β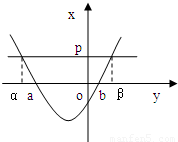
(3)解:由题意,(α-a)(α-b)=p
∴g(α)=(α-a)(α-b)(α-c)-(m+n+p)α+(am+bn+cp)=(a-α)m+(b-α)n,
∵a>α,b>α,m>0,n>0
∴g(α)>0
同理g(β)=(a-β)m+(b-β)n,
∵a<β,b<β,m>0,n>0
∴g(β)<0
故g(α)是正数,g(β)是负数.
点评:本题以二次函数为载体,考查方程根的判断,考查函数值符号的确定,同时考查了数形结合的数学思想,难度一般.
(2)方程f(x)=p的两根为α、β(α<β),即y=f(x)与y=p的图象交点的横坐标为α、β,又y=f(x)与y=0的图象交点的横坐标为a,b(a>b),且y=f(x)的图象开口向上,从而可得结论;
(3)由题意,(α-a)(α-b)=p,g(α)=(a-α)m+(b-α)n,根据a>α,b>α,m>0,n>0,可得g(α)>0;同理g(β)=(a-β)m+(b-β)n,根据a<β,b<β,m>0,n>0,可得g(β)<0.
解答:(1)证明:由f(x)=p,可化为x2+(a+b)x+ab-p=0
∵△=(a+b)2-4(ab-p)=(a-b)2+4p,p>0
∴△>0
故方程f(x)=p有两个不等实数根
( 2)解:方程f(x)=p的两根为α、β(α<β),即y=f(x)与y=p的图象交点的横坐标为α、β,又y=f(x)与y=0的图象交点的横坐标为a,b(a>b),且y=f(x)的图象开口向上,如图所示,可知α<a<b<β

(3)解:由题意,(α-a)(α-b)=p
∴g(α)=(α-a)(α-b)(α-c)-(m+n+p)α+(am+bn+cp)=(a-α)m+(b-α)n,
∵a>α,b>α,m>0,n>0
∴g(α)>0
同理g(β)=(a-β)m+(b-β)n,
∵a<β,b<β,m>0,n>0
∴g(β)<0
故g(α)是正数,g(β)是负数.
点评:本题以二次函数为载体,考查方程根的判断,考查函数值符号的确定,同时考查了数形结合的数学思想,难度一般.

练习册系列答案
相关题目
 =c
=c <c
<c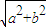 >c
>c