题目内容
如图,设AB为⊙O的任一条不与直线l垂直的直径,P是⊙O与l的公共点,AC⊥l,BD⊥l,垂足分别为C,D,且PC=PD,求证: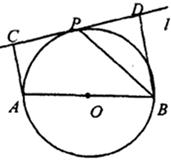
(1)l是⊙O的切线;
(2)PB平分∠ABD.
(1)见解析;(2)见解析.
解析试题分析:(1)连结OP,通过证明OP//BD得OP⊥l.,从而l是⊙O的切线;(2)连结AP,由(1)知l是⊙O的切线所以∠BPD=∠BAP,又∠BPD+∠PBD=90°,∠BAP+∠PBA=90°,所以∠PBA=∠PBD,即PB平分∠ABD.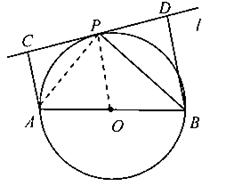
试题解析:(1)连结OP,
因为AC⊥l,BD⊥l, 所以AC//BD.
又OA=OB,PC=PD, 所以OP//BD,从而OP⊥l.
因为P在⊙O上, 所以l是⊙O的切线. ...........5分
(2)连结AP,
因为l是⊙O的切线, 所以∠BPD=∠BAP.
又∠BPD+∠PBD=90°,∠BAP+∠PBA=90°,
所以∠PBA=∠PBD,即PB平分∠ABD. .........10分
考点:圆的切线、几何证明选讲.

练习册系列答案
相关题目

 中,
中, 是的中点,
是的中点,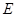 是
是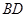 的中点,
的中点,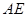 的延长线交
的延长线交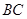 于
于 .
.
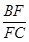 的值;
的值;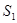 ,四边形
,四边形 的面积为
的面积为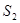 ,求
,求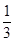 AC,AE=
AC,AE=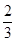 AB,BD,CE相交于点F.
AB,BD,CE相交于点F.
 、
、 、
、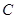 是圆
是圆 上三点,
上三点, 是
是 的角平分线,交圆
的角平分线,交圆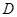 ,过
,过 .
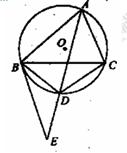
.
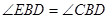 ;
;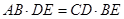 .
.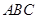 内接于⊙
内接于⊙ ,
,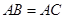 ,直线
,直线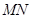 切⊙
切⊙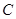 ,弦
,弦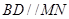 ,
, 相交于点
相交于点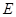 .
.
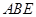 ≌△
≌△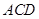 ;
;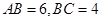 ,求
,求 长.
长. 是以
是以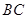 为直径的
为直径的 上一点,
上一点, 于点
于点 ,过点
,过点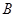 作
作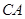 的延长线相交于点
的延长线相交于点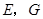 是
是 的中点,连结
的中点,连结 并延长与
并延长与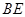 相交于点
相交于点 ,延长
,延长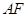 与
与 的延长线相交于点
的延长线相交于点 .
.
 ;
; 是
是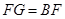 ,且
,且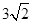 ,求
,求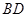 和
和 的长度.
的长度.