题目内容
要使直线y=kx+1（k∈R）与焦点在x轴上的椭圆
+
=1总有公共点，实数a的取值范围是（ ）
| x2 |
| 7 |
| y2 |
| a |
| A、0＜a≤1 |
| B、0＜a＜7 |
| C、1≤a＜7 |
| D、1＜a≤7 |
分析：由题意直线y=kx+1恒过定点M（0，1），要使直线y=kx+1（k∈R）与焦点在x轴上的椭圆
+
=1总有公共点，则只需要点M（0，1）在椭圆上或椭圆内，代入可求
| x2 |
| 7 |
| y2 |
| a |
解答：解：由题意直线y=kx+1恒过定点M（0，1）
要使直线y=kx+1（k∈R）与焦点在x轴上的椭圆
+
=1总有公共点
则只需要点M（0，1）在椭圆上或椭圆内
则
≤1且a＜7
∴1≤a＜7
故选：C
要使直线y=kx+1（k∈R）与焦点在x轴上的椭圆
| x2 |
| 7 |
| y2 |
| a |
则只需要点M（0，1）在椭圆上或椭圆内
则
| 1 |
| a |
∴1≤a＜7
故选：C
点评：本题主要考查了直线与椭圆位置关系的判断，常见的判断方法是联立直线方程与曲线方程，但此类方法一般计算量比较大，而本题的这种解决灵活的应用了直线恒过定点的性质，但解题时容易漏洞焦点在x轴上的条件的考虑，误认为只有a≥1
练习册系列答案
相关题目
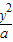=1总有公共点，则实数a的取值范围是（ ）
C.1≤a＜
D.1＜a≤
+
=1总有公共点，实数a的取值范围是（ ）
+
=1总有公共点，实数a的取值范围是（ ）