题目内容
已知椭圆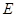 的中心在坐标原点,焦点在
的中心在坐标原点,焦点在 轴上,离心率为
轴上,离心率为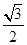 ,且过双曲线
,且过双曲线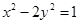 的顶点.
的顶点.
(1)求椭圆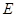 的标准方程;
的标准方程;
(2)命题:“设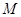 、
、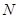 是双曲线
是双曲线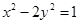 上关于它的中心对称的任意两点,
上关于它的中心对称的任意两点,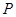 为该双曲线上的动点,若直线
为该双曲线上的动点,若直线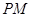 、
、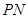 均存在斜率,则它们的斜率之积为定值”.试类比上述命题,写出一个关于椭圆
均存在斜率,则它们的斜率之积为定值”.试类比上述命题,写出一个关于椭圆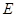 的类似的正确命题,并加以证明和求出此定值;
的类似的正确命题,并加以证明和求出此定值;
(3)试推广(Ⅱ)中的命题,写出关于方程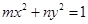 (
(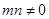 ,
,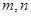 不同时为负数)的曲线的统一的一般性命题(不必证明).
不同时为负数)的曲线的统一的一般性命题(不必证明).
(1)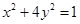 .
.
(2)关于椭圆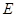 的正确命题是:设
的正确命题是:设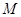 、
、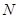 是椭圆
是椭圆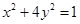 上关于它
上关于它
的中心对称的任意两点,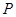 为该椭圆上的动点,若直线
为该椭圆上的动点,若直线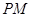 、
、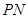 均存在斜率,
均存在斜率,
则它们的斜率之积为定值.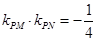 (定值)
(定值)
(3)关于方程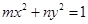 (
(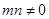 ,
,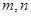 不同时为负数)的曲线的统一的一般性命题是:
不同时为负数)的曲线的统一的一般性命题是:
设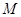 、
、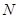 是方程
是方程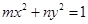 (
(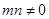 ,
,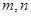 不同时为负数)的曲线上关于它的中心对称的任意两点,
不同时为负数)的曲线上关于它的中心对称的任意两点,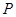 为该曲线上的动点,若直线
为该曲线上的动点,若直线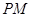 、
、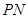 均存在斜率,则它们的斜率之积为定值.
均存在斜率,则它们的斜率之积为定值.
解析试题分析:(1)设椭圆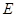 的方程为
的方程为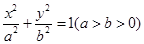 ,半焦距为
,半焦距为 ,
,
则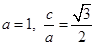 ,
,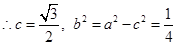 ,
, 椭圆
椭圆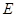 的方程为
的方程为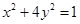 .
.
(2)关于椭圆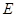 的正确命题是:设
的正确命题是:设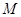 、
、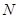 是椭圆
是椭圆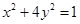 上关于它
上关于它
的中心对称的任意两点,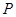 为该椭圆上的动点,若直线
为该椭圆上的动点,若直线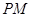 、
、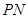 均存在斜率,
均存在斜率,
则它们的斜率之积为定值.
证明如下:
设点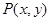 ,
,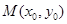 ,
,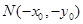 ,
,
直线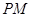 、
、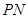 的斜率分别为
的斜率分别为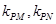 ,
,
则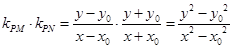 ,
,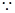 点
点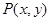 ,
,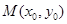 在椭圆上,
在椭圆上,
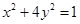 ,且
,且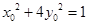 ,
,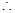
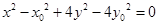 , 即
, 即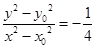 ,
,
所以,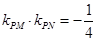 (定值)
(定值)
(3)关于方程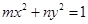 (
(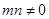 ,
,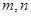 不同时为负数)的曲线的统一的一般性命题是:
不同时为负数)的曲线的统一的一般性命题是:
设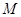 、
、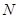 是方程
是方程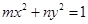 (
(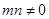 ,
,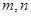 不同时为负数)的曲线上关于它的中心对称的任意两点,
不同时为负数)的曲线上关于它的中心对称的任意两点,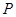 为该曲线上的动点,若直线
为该曲线上的动点,若直线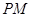 、
、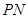 均存在斜率,则它们的斜率之积为定值.
均存在斜率,则它们的斜率之积为定值.
考点:本题主要考查椭圆的标准方程,直线与椭圆的位置关系。
点评:中档题,求椭圆的标准方程,主要运用了椭圆的几何性质,注意明确焦点轴和a,b,c的关系。曲线关系问题,往往通过联立方程组,得到一元二次方程,运用韦达定理。本题(2)注意将斜率用坐标表示出来,易于发现关系。本题得到一般性结论,对指导学生学习探究很有裨益。

 :
: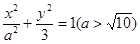 的右焦点
的右焦点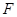 在圆
在圆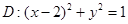 上,直线
上,直线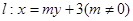 交椭圆于
交椭圆于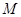 、
、 两点.
两点.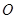 为坐标原点),求
为坐标原点),求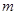 的值;
的值; 设点
设点 轴的对称点为
轴的对称点为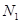 (
( ,试问
,试问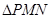 的面积是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由.
的面积是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由.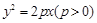 的焦点为
的焦点为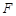 ,点
,点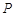 是抛物线上的一点,且其纵坐标为4,
是抛物线上的一点,且其纵坐标为4,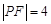 .
.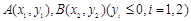 是抛物线上的两点,
是抛物线上的两点,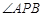 的角平分线与
的角平分线与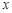 轴垂直,求直线AB的斜率;
轴垂直,求直线AB的斜率;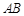 过点
过点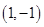 ,求弦
,求弦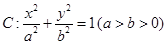 .
.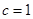 ,且
,且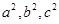 成等差数列,求椭圆
成等差数列,求椭圆 的方程;
的方程;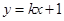 相交于
相交于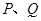 两点,求
两点,求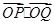 的取值范围.
的取值范围. ,
,
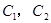 的方程为普通方程,并说明它们分别表示什么曲线?
的方程为普通方程,并说明它们分别表示什么曲线?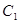 上的点P对应的参数为
上的点P对应的参数为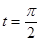 ,Q为
,Q为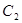 上的动点,求PQ的中点M到直线
上的动点,求PQ的中点M到直线 的距离的最小值
的距离的最小值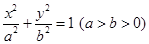 过点
过点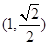 ,离心率为
,离心率为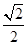 ,左、右焦点分别为
,左、右焦点分别为 、
、 .点
.点 为直线
为直线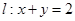 上且不在
上且不在 轴上的任意一点,直线
轴上的任意一点,直线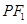 和
和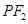 与椭圆的交点分别为
与椭圆的交点分别为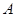 、
、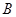 和
和 、
、 ,
, 为坐标原点.设直线
为坐标原点.设直线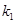 、
、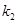 .
.
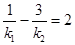 ;
;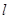 上是否存在点
上是否存在点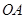 、
、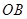 、
、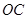 、
、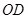 的斜率
的斜率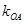 、
、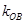 、
、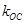 、
、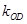 满足
满足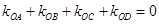 ?若存在,求出所有满足条件的点
?若存在,求出所有满足条件的点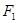 、
、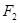 分别为椭圆
分别为椭圆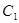 :
: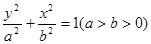 的上、下焦点,其中
的上、下焦点,其中 :
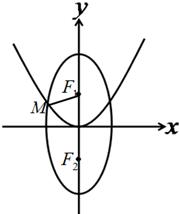
: 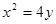 的焦点,点
的焦点,点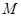 是
是 。
。
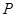 (1,3)和圆
(1,3)和圆 :
: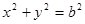 ,过点
,过点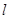 与圆
与圆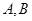 ,在线段
,在线段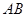 取一点
取一点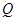 ,满足:
,满足: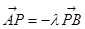 ,
,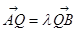 (
(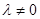 且
且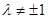 )。
)。 的右焦点为
的右焦点为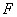 ,右准线为
,右准线为 ,离心率为
,离心率为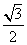 ,点
,点 在椭圆上,以
在椭圆上,以 为半径的圆与
为半径的圆与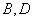 .
.
 是边长为
是边长为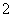 的等边三角形,求圆的方程;
的等边三角形,求圆的方程;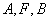 三点在同一条直线
三点在同一条直线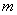 上,且原点到直线
上,且原点到直线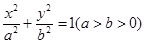 的左右焦点分别为
的左右焦点分别为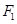 、
、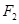 ,由4个点
,由4个点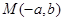 、
、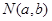 、
、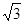 ,面积为
,面积为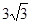 的等腰梯形.
的等腰梯形.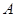 、
、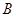 两点,求
两点,求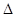
 面积的最大值.
面积的最大值.