题目内容
已知两定点 和
和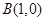 ,动点
,动点 在直线
在直线 上移动,椭圆
上移动,椭圆 以
以 为焦点且经过点
为焦点且经过点 ,记椭圆
,记椭圆 的离心率为
的离心率为 ,则函数
,则函数 的大致图像是( )
的大致图像是( )
A
解析试题分析:根据题意,两定点 和
和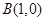 ,动点
,动点 在直线
在直线 上移动,椭圆
上移动,椭圆 以
以 为焦点且经过点
为焦点且经过点 ,记椭圆
,记椭圆 的离心率为
的离心率为 ,因为2c=2,c=1,且2a利用对称性可知,,先求解点A关于直线y=x+2的对称点(-2,1),那么利用两点之间的最短可知2a
,因为2c=2,c=1,且2a利用对称性可知,,先求解点A关于直线y=x+2的对称点(-2,1),那么利用两点之间的最短可知2a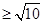 则离心率有最大值,则函数
则离心率有最大值,则函数 的大致图像是A,其余的没有的最大值,错误,故选A。
的大致图像是A,其余的没有的最大值,错误,故选A。
考点:函数图像
点评:解决的关键是理解函数的表达式,进而结合函数的思想来判定,属于中档题。

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
已知函数 有四个不同的零点,则实数
有四个不同的零点,则实数 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
设点 在曲线
在曲线 上,点
上,点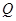 在曲线
在曲线 上,则
上,则 的最小值为( )
的最小值为( )
A. | B. | C. | D. |
函数 的图象( )
的图象( )
| A.关于原点对称 | B.关于y轴对称 |
| C.关于x轴对称 | D.关于直线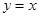 对称 对称 |
函数 的值域是( )
的值域是( )
A.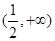 | B. | C. | D. |
已知定义在R上的函数 满足
满足 ,如图表示该函数在区间
,如图表示该函数在区间 上的图象,则
上的图象,则 等于
等于
| A.3 | B.2 | C.1 | D.0 |

 ,则
,则 的大致图象是( )
的大致图象是( )